What is gamma function?

Today we’re going to discuss one of the non-elementary functions called gamma function and consider some of its properties. Gamma function is of great importance, it’s widely applied in math (in particular, when integrating certain types of expression gamma function helps greatly, we’ll see that later in examples), also gamma function is used in probability theory (possibly, you’ve heard about gamma distribution), etc. One of the most common representations of gamma function is the following:

\Gamma(p)=\int_0^{\infty}{e^{-x}x^{p-1}dx}, p>0

This is only true for positive values of parameter p. So to obtain value of gamma function in a certain point p we need to integrate over x the expression e^{-x} x^{(p-1)}, leaving p as a free parameter. Notice limits of integration – zero and infinity. This means that we’re dealing with improper integral.

By the way, find video on Gamma function on our Youtube channel:

Although the formula written above works only for positive values of parameters, it’s still very useful and widely applied for solving problems. There’s another way to introduce gamma function:

\Gamma(p)=\frac{\Gamma(p+1)}{p}

which holds for arbitrary values of p (positive, negative or even complex!).

Let’s return to the integral representation and discuss it. First of all, notice the limits of integration:

\Gamma(p)=\int_0^{\infty}{e^{-x}x^{p-1}dx}, p>0

They are zero and infinity. The latter means we’re dealing with an improper integral. Moreover, another type of singularity appears when p<1. In this case power of x is negative, therefore the expression under the integral is undefined for lower limit of integration x=0.

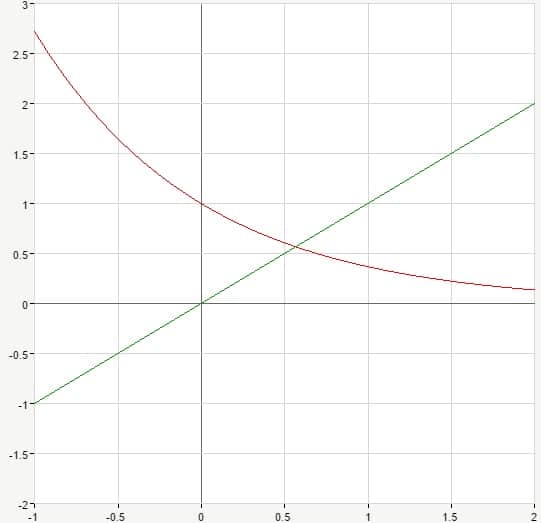
Under the integral we have a product of two functions – exponential and power function. As we know, the whole integral can be represented as the area bounded by the product curve and the horizontal axis on the interval from zero to infinity. Let’s pick a few positive integer values for parameter p and draw that area. Consider p=2:

\Gamma(2)=\int_0^{\infty}{e^{-x}x^{2-1}dx}=\int_0^{\infty}{e^{-x}xdx}

So we have an exponential function multiplied by linear function. These functions are shown on the picture below:

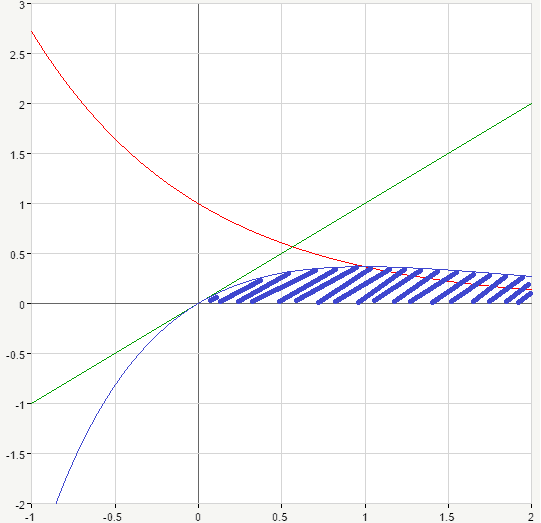
Straight line y=x is shown in green, exponential function y=e^{-x} goes in red. Ok, but how can we obtain a product curve representing the whole expression under the integral? Let’s multiply the values of these two functions for each x from zero towards infinity and thus obtain the required product curve. The resulting function is shown in blue:

So, the area bounded by the blue curve and the x-axis (shaded blue on the picture above). From the graph we can see that the product curve has intervals of increase and decrease and therefore the maximum. Let’s find its x-coordinate. For that we take the expression under the integral, find its derivative and equate it to zero. Let’s perform transformations for general case, so we can use it later:

(e^{-x}x^{p-1})’=-e^{-x}x^{p-1}+e^{-x}(p-1)x^{p-2}=e^{-x}x^{p-1}(-1+(p-1)\frac{1}{x})=0

As we know, exponential function never turns zero (look at the graph above if you’re not sure about this). Also we can say that $x$ should not equal to zero as well, because it stands in the denominator. Therefore we’re to solve the following simplified equation for x:

-1+(p-1)\frac{1}{x}=0

(p-1)\frac{1}{x}=1

x_{max}=p-1

This is the x-coordinate of a maximum for the product curve.

So for the case we have been considering we obtain the following:

x_{max}=2-1=1

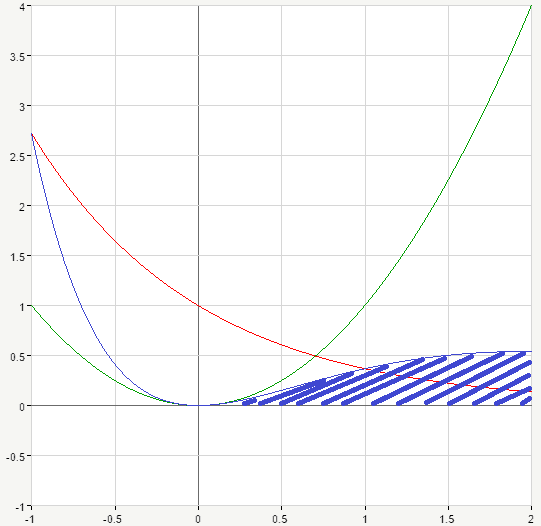
Ok, now let’s move on and pick another value of parameter p, say let p=3. So we’ll have:

\Gamma(3)=\int_0^{\infty}{e^{-x}x^{3-1}dx}=\int_0^{\infty}{e^{-x^2}xdx}

This time we have an exponential function multiplied by quadratic function. Again, let’s graph them:

Product curve goes in blue again, and the shaded area represent the value of the whole integral. As we can see from those two graphs, value of \Gamma-function increases with the increase of the p-parameter.

Ok, hopefully, you’ve got now some idea of how gamma function behaves depending on parameter p. What’s really important is that gamma function is closely related to the notion of factorial. For positive integer arguments n gamma function can be written in the following form:

\Gamma(n)=\int_{0}^{\infty}e^{-x}x^{n-1}dx

where $n$ is a positive integer. Hence:

\Gamma(n+1)=\int_{0}^{\infty}e^{-x}x^{n+1-1}dx=\int_{0}^{\infty}e^{-x}x^{n}dx

Let’s evaluate this integral applying integration by parts:

\begin{aligned} \int_{0}^{\infty}e^{-x}x^{n}dx=\begin{vmatrix}u=x^n\\du=nx^{n-1}dx \\dv=e^{-x}dx\\v=-e^{-x}\end{vmatrix}=-e^{-x}x^n\left.\begin{matrix}\end{matrix}\right| _0^{\infty}-\int_{0}^{\infty}{(-e^{-x})nx^{n-1}dx}=&\\0+n\int_0^{\infty}{e^{-x}x^{n-1}dx}=n\Gamma(n)\end{aligned}

So, we’ve just shown the following:

\Gamma(n+1)=n\Gamma(n)

This is the recurrent formula. Which is, if we only knew \Gamma(n-1), we could evaluate \Gamma(n). Actually, since n is arbitrary, we can rewrite it as follows:

\Gamma(n)=(n-1)\Gamma(n-1)

Now we can substitute this expression into the previous formula instead of \Gamma(n) and we’ll have:

\Gamma(n+1)=n(n-1)\Gamma(n-1)

Similarly:

\Gamma(n-1)=(n-2)\Gamma(n-2)

Substituting again:

\Gamma(n+1)=n(n-1)(n-2)\Gamma(n-2)

We can go on doing that until finally we obtain the following:

\Gamma(2)=1\cdot \Gamma(1)

$\Gamma(1)$ can be evaluated, let’s find it:

\Gamma(1)=\int_0^{\infty}{e^{-x}x^{1-1}dx}=\int_0^{\infty}{e^{-x}dx}=-e^{-x}\left.\begin{matrix}\end{matrix}\right| _0^{\infty}=0-(-1)=1

So, updating our general formula, we obtain:

\Gamma(n+1)=n(n-1)(n-2)…2\cdot 1=n!

We’ve shown that \Gamma(n+1)=n!, so gamma function is equal to the value of factorial for positive integer arguments.

Up to this moment we have only considered positive values of parameter p. But what if we try, for example, negative numbers? That is where the following formula comes in handy:

\Gamma(p)=\frac{\Gamma(p+1)}{p}

As we’ve mentioned at the very beginning, this representation is valid for any value of parameter p, even for complex. So, it turns out that gamma function generalizes the notion of factorial on fractional, negative and even complex numbers.

Now let’s consider some important properties of gamma function.

Euler’s reflection formula:

\Gamma(p)\cdot \Gamma(1-p)=\frac{\pi}{\sin{\pi p}}, p\in (0,1)

 Duplication formula:

2^{p-1}\Gamma(\frac{p}{2})\Gamma(\frac{p+1}{2})=\sqrt{\pi}\Gamma(p)

If we substitute $p=1$ into this formula we’ll obtain the following:

2^{1-1}\Gamma(\frac{1}{2})\Gamma(\frac{1+1}{2})=\sqrt{\pi}\Gamma(1)

1\cdot \Gamma(\frac{1}{2})\Gamma(1)=\sqrt{\pi}\Gamma(1)

\Gamma(\frac{1}{2})=\sqrt{\pi}

Also there’s interconnection between gamma and beta function (we’ll discuss the latter in one of our next sections):

B(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}

So beta function can be expressed as a combination of gamma functions. Let’s try to understand why it is so. Beta function for positive integer arguments m, n can be written as follows:

B(m,n)=\frac{(m-1)!(n-1)!}{(m+n-1)!}

We also know that

\Gamma(n+1)=n!

\Gamma(n)=(n-1)!

Taking that into consideration, we obtain:

B(m,n)=\frac{\Gamma(m)\Gamma(n)}{\Gamma(n+1)}

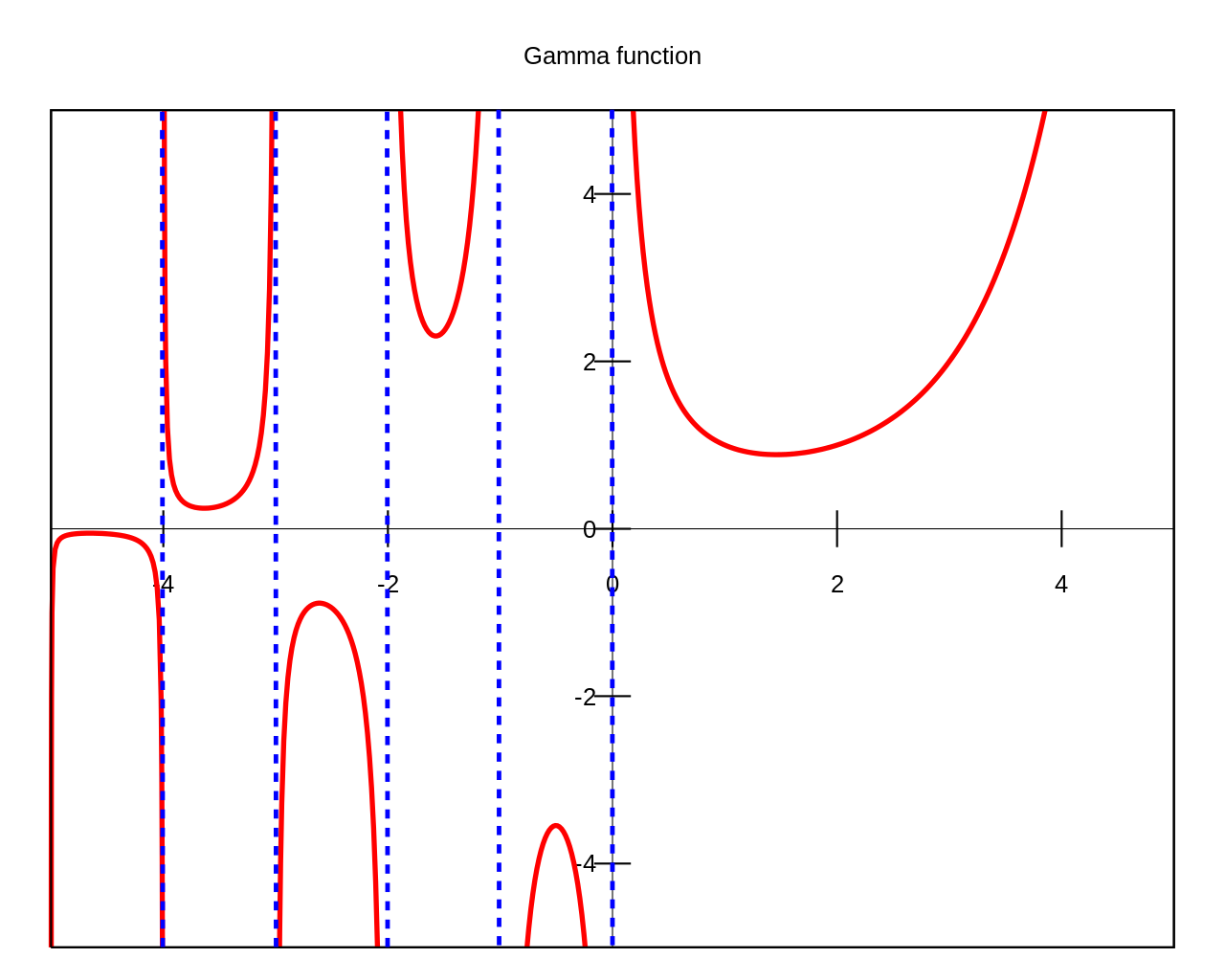
Now let’s talk about how gamma function looks like in case of real argument. Note that gamma function cannot be expressed with the help of  elementary functions, i.e. we cannot write it as some combination of familiar functions (exponents, trigonometry, etc.).

If we look on its right, we’ll notice that gamma function is continuous for positive values of the argument.  But for p=0 or p<0 gamma function has singularity points. Let’s see why.

\Gamma(p)=\frac{\Gamma(p+1)}{p}

If we substitute p=0 we’ll obtain:

\Gamma(0)=\frac{\Gamma(0+1)}{0}=\frac{\Gamma(1)}{0}=\frac{1}{0}=\infty

Ok, let’s have a closer look at it. Consider p=+0 which is not actually zero but a very small positive number:

\Gamma(+0)=\frac{1}{+0}=+\infty

Doing the same for $p=-0$ which is a very small by absolute value negative number:

\Gamma(-0)=\frac{1}{-0}=-\infty

And that is exactly what we have on a graph. If p-parameter is approaching zero from the right gamma function tends to positive infinity. When p is approaching zero from the left gamma function tends to negative infinity.  Now let’s consider values of gamma function for negative integer arguments -k, where k is positive integer. We’re going to apply recurrent formula for gamma function consequently for the numerator:

\Gamma(-k)=\frac{\Gamma(-k+1)}{-k}=\frac{1}{-k}\frac{\Gamma(-k+2)}{-k+1}=\frac{1}{-k}\frac{1}{-k+1}\frac{\Gamma(-k+3)}{-k+2}=…=\frac{(-1)^k \Gamma(0)}{k!}

We’ve already shown that \Gamma(0)=\infty and therefore for each negative integer value of the argument of gamma function we’ll obtain positive or negative infinity. Moreover, there are no other singularity points of gamma function of real argument other than these.

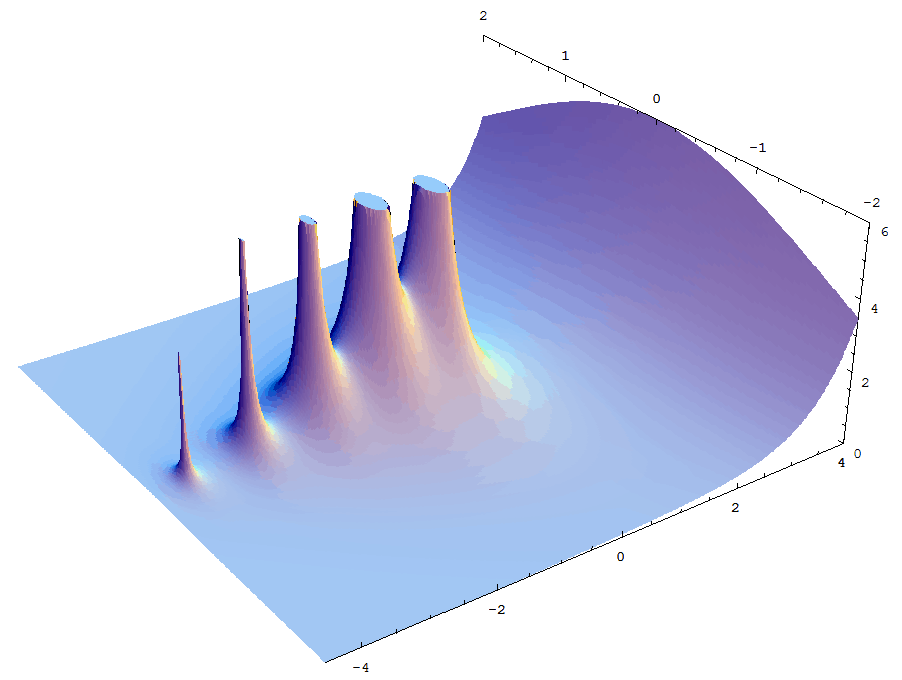
And here’s how complex gamma function looks like:

You may ask, ok, this is great, but how can I use gamma functions? As it turns out, they really come in handy, for example, for integration of certain expressions, we’ll discuss it in one of the next sections and now you can check our video example showing how to evaluate this not so easy looking integral \int_0^{\infty}{x^{\frac{1}{2}}e^{-x^{1/6}}}dx applying gamma functions.