What is beta function?

In this section we’re continuing to discuss non-elementary functions called Euler integrals. These special functions are widely used in mathematics and physics. It was once discovered that they describe properties of elementary particles in the string theory. We won’t dig into this amazing topic today, though. For starters let’s talk about what is beta function and define its key properties for solving problems in math. Basically, later we’ll show you how these functions can simplify the evaluation process of certain pretty complicated integrals.

Here’s the Euler integral of the first kind, which is also known as beta function:

B(p,q)=\int_0^{1}{x^{p-1}(1-x)^{q-1}dx}

where p and q are parameters.

Beta function is closely connected with gamma function discussed earlier. In fact, beta function can be expressed through several gamma function of different arguments, we’ll discuss the exact formula later in this article.

If p<1, q<1 then this is an improper integral meaning that it has singularity points. Let’s see. In such case power we have next to x and 1-x become negative numbers which is exactly the same as if we have these two factors in the denominator. If either of them equals zero, the whole expression under the integral approaches infinity.

Check the video version of this tutorial on our youtube channel:

Now let’s consider the expression we have under the integral. It may look complicated, but what we actually have here is a product of two polynomials x^{p-1} and (1-x)^{q-1}. Let’s discuss them.

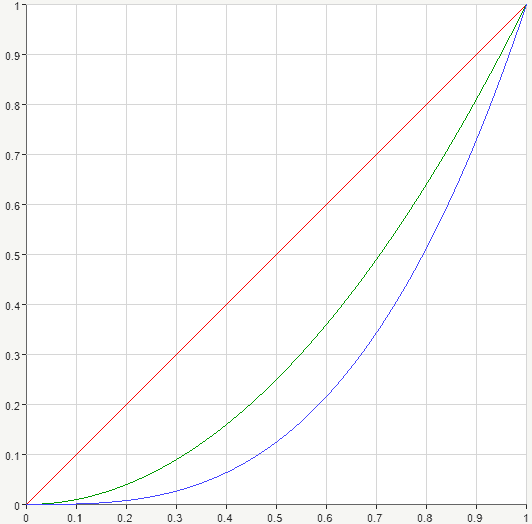
The limits of integration are [0,1], therefore, the expression x^{p-1} takes only non-negative values. Now let’s take a few integer values for the p parameter and graph these curves.

For p=2 we’ll have simply x, p=3 yields x^2, if p=4 we have x^3. Let’s graph these curves. We have a straight line, a parabola and a cubic function here.

Notice that no matter what value takes parameter p, integer or fractional, these curves will still pass through the two points (0,0) and (1,1). And that’s natural, let’s see! Substitute zero and 1:

0^{p-1}=1, 1^{p-1}=1

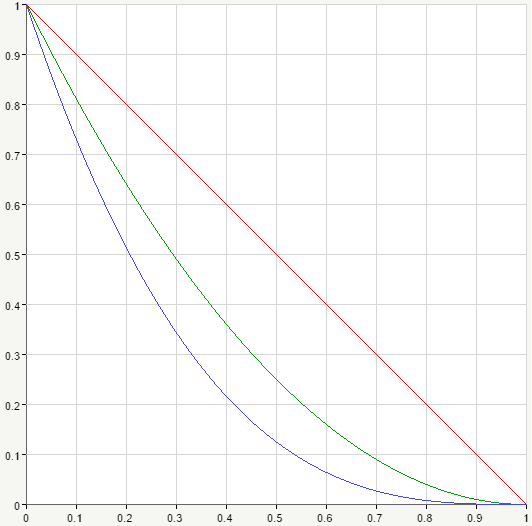
Now let’s move on to the second factor. We can see that it’s also a positive number for the given limits of integration [0,1] as x never exceeds 1. Let’s take a few integer values for the q parameter. When q=2, we obtain 1-x. For q=3 we get (1-x)^2. And q=4 yields (1-x)^3. And again, we have a straight line, a parabola and a cubic function.

We can see once again, that no matter value the parameter q takes, these curves still pass through the points (0,1) and (1,0). For x=0 we have (1-0)^{q-1}=1. If x=1 we get (1-1)^{q-1}=0. We may say that the second factor gives us the curves of the same shape as the first one, only that they’re decreasing and shifted by one to the right.

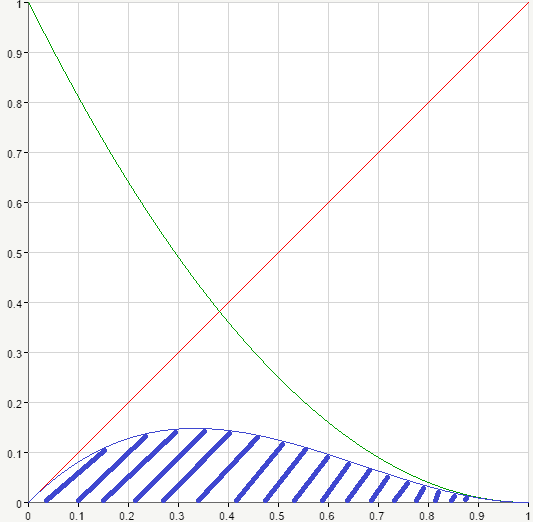
It turns out that under the integral we have a new curve of some kind and we’re asked to find the area bounded by this curve and the x-axis within the given interval x\in [0,1]. Let’s try to graph this area. Suppose p=2, q=3. This way we’ll have the following beta function:

B(2,3)=\int_0^{1}{x^{2-1}(1-x)^{3-1}dx}=\int_0^{1}{x(1-x)^{2}dx}

Thus, we have a straight line multiplied by parabola. Let’s multiply them and obtain the product curve and thus the required area.

On the picture you can see the required area dashed in blue.

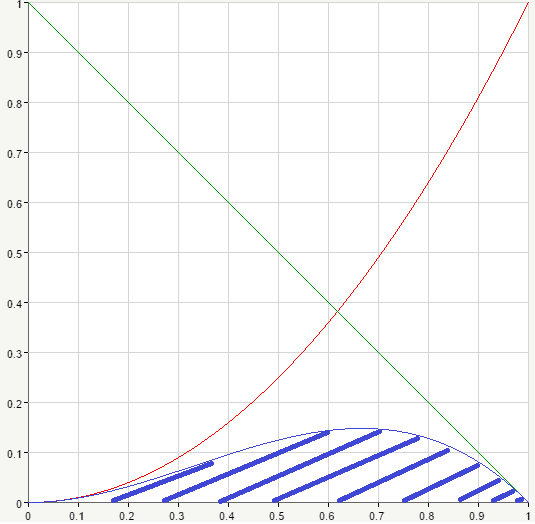
Now let’s switch the values of parameters in our formula and see what happens. So p=3, q=2 and we consider the following beta function:

B(3,2)=\int_0^{1}{x^{3-1}(1-x)^{2-1}dx}=\int_0^{1}{x^2(1-x)dx}

Again we have a parabola multiplied by a straight line. Let’s graph these two curves. Again, the product curve goes and blue.

If we look closely at the two graphs, it appears that it’s basically the same thing, they’re reflections of each other. And it’s true, switching p and q parameters never actually affects the value of beta function. Let’s prove that.

We make a substitution x=1-t, hence dx=-dt. Notice also that limits of integration are changed as well: for x=0 we get t=1-0=1, for x=1 the new limit is t=1-1=0. So we’ll have:

\begin{aligned} B(p,q)=\int_0^1{x^{p-1} (1-x)^{q-1}dx}=\int_1^0{(1-t)^{p-1} (1-(1-t))^{q-1}(-dt)}&\\=\int_0^1{(1-t)^{p-1} t^{q-1}dt}=B(q,p)\end{aligned}

Notice that we exchange upper and lower limits and, therefore, the minus sign in front of the integral disappears.
Considered property is called symmetry property of beta function according to its arguments. It means that we can swap arguments and value of the function won’t change.

Now let’s move to the next important property of function B(p,q).
Consider B(p,q+1) (we assume that p,q are positive).

B(p,q+1)=\int_0^1{x^(p-1) (1-x)^(q+1-1)dx}=\int_0^1{x^(p-1) (1-x)^q dx}

Applying integration by parts and taking into account that x^p=x^(p-1)-x^(p-1) (1-x) we’ll obtain:

\begin{aligned}B(p,q+1)=\int_0^1 {x^(p-1) (1-x)^q dx}=(\frac{x^p}{p} (1-x)^p )\left.\begin{matrix}\end{matrix}\right| _0^{1}+\frac{q}{p} \int_0^1{x^p (1-x)^(q-1)dx}=&\\ \frac{q}{p} \int_0^1{x^(p-1) (1-x)^(q-1)-x^(p-1) (1-x)^q dx}=\frac{q}{p} B(p,q)-\frac{q}{p} B(p,q+1)\end{aligned}

whence we can get the following formula:

B(p,q+1)=\frac{q}{p+q} B(p,q)

And similarly:

B(p+1,q)=\frac{p}{p+q} B(p,q)

In the same way the following formulas can be obtained:

B(p,q)=\frac{p-1}{p+q-1} B(p-1,q)

B(p,q)=\frac{q-1}{p+q-1} B(p,q-1)

Obtained results allow to reduce evaluation of B(p,q) for the case of arbitrary positive p, q to calculation of B(p,q) for p>0, q\ge 1.

If q equals to integer n then consequently applying the formula

B(p,q+1)=\frac{q}{p+q} B(p,q)

we obtain:

B(p,n)=\frac{n-1}{p+n-1}\cdot \frac{n-2}{p+n-2}…\frac{1}{p+1} B(p,1)

Since B(p,1)=\int_0^1{x^{p-1}} =\frac{1}{p} x^p \left.\begin{matrix}\end{matrix}\right| _0^{1}=\frac{1}{p}

then:

B(p,n)=\frac{1*2*3…(q-1)}{q(q+1)…(q+n-1)}

If q also equals integer m then:

B(m,n)=\frac{(n-1)!(m-1)!}{(m+n-1)!}

And, finally, there is interconnection between gamma and beta functions. It’s expressed by the following formula:

B(p,q)=\frac{Γ(p)Γ(q)}{Γ(p+q)}

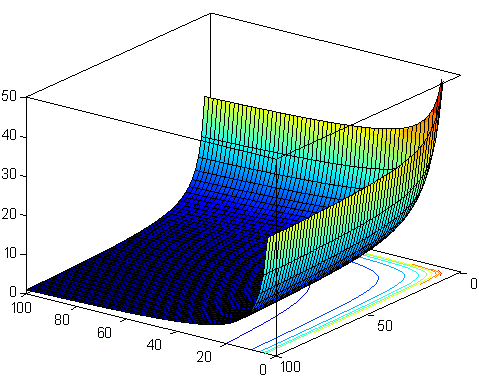
So beta function is expressed as combination of some gamma functions. Below you can see a plot of beta function for positive values of both arguments:

Beta function can come in handy for integration of certain functions, check an example of how to apply beta function on our youtube channel.