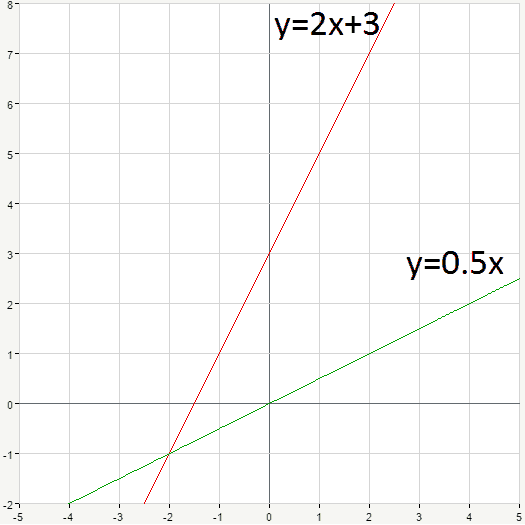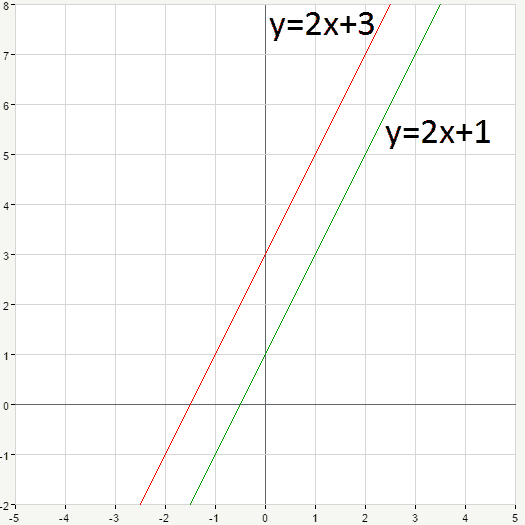One of common tasks in algebra homework is to solve a system of two linear equations. Along with other methods, we can do it graphically. This section is devoted to intersection of two straight lines on a plane. In other words, let’s talk about solving a system of two linear equations. As we discussed earlier, a straight line on a plane is described by the following equation:
y=kx+b
This equation sets a certain dependence between coordinates $x$ and $y$ of the point lying on this line. So, if we want to discuss intersection of two lines, we’ll have to deal with two equations of such kind.
Consider the following system:
\left\{ \begin{aligned}y=2x+3\\x-2y=0 \end{aligned}\right.
Each of the two linear equations represents a straight line, so let’s graph them.
The first equation has y-intercept b=3, thus we have point (0,3).
Slope m=2=\frac{2}{1}, thus the second point is (1,5). How did we get this? Recall the rise-over-run formula for the slope:
m=\frac{rise}{run}
Rise means increase in y coordinate, run goes for increase in x coordinate. Thus, in our case when x “runs” for 1, y “rises” for 2. So, (0,3) \rightarrow (0+1,3+2)=(1,5). That’s our second point.
Let’s take a look at the second equation. We should solve it for y first:
x-2y = 0 \rightarrow -2y=-x \rightarrow y=0.5x
Ok, now we finally have this equation in slope-intercept form, y-intercept b=0 (that’s because the corresponding term is absent in the equation, we have just 0.5x in the right part), slope m=0.5=\frac{1}{2}. Thus, the points are (0,2), (1,0.5).
Check also video tutorial on our youtube channel:

As we have a pair of points for each line, we can easily graph them:
We’ve already discussed that a solution of single linear equation is every point lying on the line which represents that equation. If we consider a system of two equations, the solution of such system will be the point lying on both lines at the same time. We can see from the graph that our lines have only one common point, they intersect at (-2,-1). Therefore, the solution of our systems of equations is x=-2, y=-1.
In general, not every system of two linear equations has single solution like in our example. Our two lines intersected, but that’s not always the case. Two lines on a plane can either be parallel or coincide, or intersect at a single point.
Let’s take a look at some examples.
Two parallel lines
Consider the following pair of lines:
\left\{ \begin{aligned}y=2x+3\\y=2x+1 \end{aligned}\right.
The first one is the same as in previous example. Consider the second equation. The y-intercept is b=1, thus we have the point (0,1). The slope m is the same as for the first line: m=2, therefore the second point is (1,3). Two points are enough to graph a line, as we know. Look at the graph:
Here are two parallel lines which never intercept. Hence, the system of equations has no solution at all.
As we know, slope m shows how steep the line is. If two lines have the same slopes they are of the same steepness and thus parallel, like in our case.
Coinciding lines
\left\{ \begin{aligned}y=2x+3\\4x-2y+6=0 \end{aligned}\right.
At first let’s solve the second equation for y:
4x-2y+6 = 0 \rightarrow 4x+6=2y
Diving by 2 both parts of equation we obtain:
2x+3=y
or in usual form:
y=2x+3
Now our system of equations looks like this:
\left\{ \begin{aligned}y=2x+3\\y=2x+3 \end{aligned}\right.
Thus, the two equations of the system are the same. It means that when drawn on the plane they will coincide. Every point of the two coinciding lines is a solution of the system. In this case it’s said that a system has infinite number of solutions.
Summing up. If you’re asked to solve a system of two linear equations, this means you are dealing with two lines. Solution of a system is a set of points at which these two lines intersect. Three cases are possible:
– two lines intersect at just one point. The system has unique solution.
– the lines are parallel, they never meet and have no common points, thus the system has no solutions.
– the lines coincide, i.e. they are represented by identical equations. Each point of one line also belongs to another. In this case the system has infinitely many solutions.
That’s what you need to know about intersection of two lines on a plane and their connection with system of two linear equations. Still have questions? Concerned with any other math, physics, chemistry problems in your homework? Just let us know, we’re ready to help.