Let’s talk about straight lines on a plane. We often answer questions of our visitors about how to graph a line and other related stuff. For example, recently we were asked how to graph y=2x+3. To answer this question let’s consider equation of a straight line or so called linear equation on the plane. For that we will need a coordinate plane. It is formed by a horizontal number line called the x-axis and a vertical number line called the y-axis. The two axes intersect at a point called the origin. That’s not all. To define coordinates we should chose the scale:
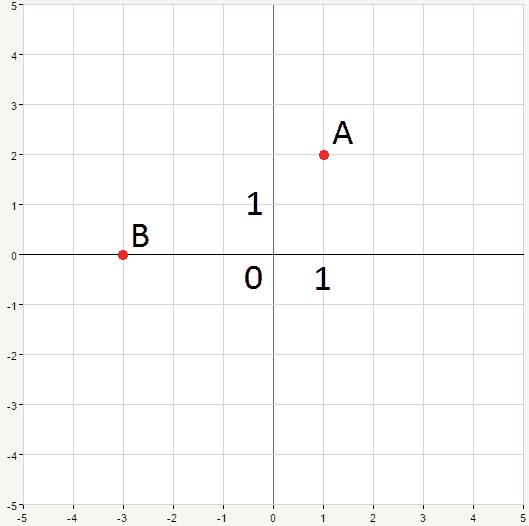
Now we can locate any point on the plane by an ordered pair of numbers (x,y), called the coordinates. For example, point A on the picture below has coordinates (2,2), and point B has coordinates (-3,0):
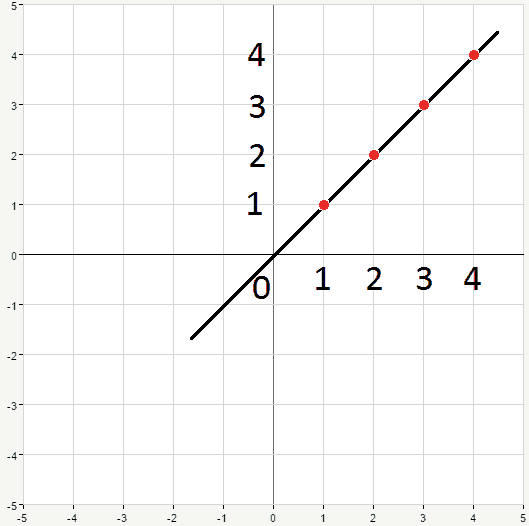
The first number in pair stands for x coordinate and the second for y. If we connect these two points, we’ll obtain a line. Now, all the points located on that line have something in common. There’s a certain dependency between their y coordinates and x coordinates. This dependency can be expressed as an equation. Ok, let’s graph some lines. We’ll start with the simplest case: y=x. Let’s pick a couple of values for the x coordinate and find corresponding values for y (according to the given equation):
\begin{matrix} x&y\\ \\ 1&1\\2&2 \\3&3\\4&4\end{matrix}
Now graph the points and connect them obtaining a straight line:
You can see that, basically, two points would suffice to draw a straight line, because it won’t turn anyway at some point, it’s straight. So, all we need to do is to fix the direction. Take a look at another example, the equation is y=2x. We only need two points:
\begin{matrix} x&y\\ \\ 1&2\\2&4\end{matrix}
Marking them on the plane and carefully connecting we obtain the desired graph:
As you can see from the graph, our second line is steeper than the first one. Let’s move on and consider the equation from our visitor’s question:
y=2x+3
Obviously, it’s yet another equation of a straight line. This equation means that every point lying on the corresponding line has coordinates which satisfy the given equation.
Check video-tutorial about lines on our youtube channel:
For example, point (-1,1) lies on this line, because if we substitute the coordinates we obtain:
1=-1\cdot 2+3 \rightarrow 1=1
which is obviously true.
Point (1,2) does not belong to the given line because 2\cdot 1+3=2 \rightarrow 5=2
and that’s false.
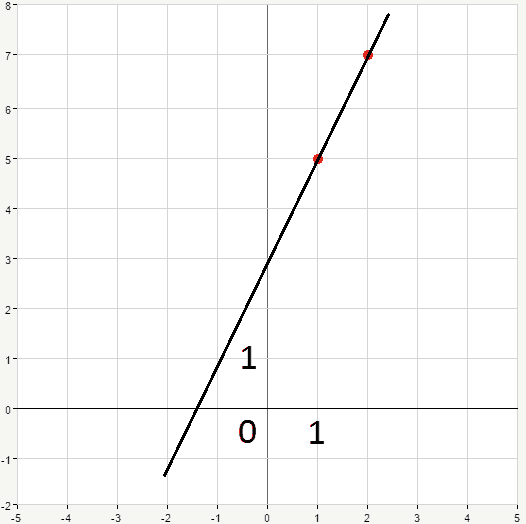
Let’s take, for example, x=1. Substituting it into the initial equation we get:
y-2\cdot 1=3 \rightarrow y=2+3=5
Hence, the first point is (1,5)
x=2: y-2\cdot 2=3 \rightarrow y=4+3=7
So, the second point is (2,7). Having two points we can draw a line through them:
If we replace the numbers in our last example by parameters m and b we’ll get the following equation:
y=mx+b
This is an equation of a straight line in general form which is called the slope-intercept form. What does it stand for?
b is called y-intercept and simply shows where the line crosses y-axis.
m defines how change of y depends on change of x and is called a slope. In other words, slope shows how steep the line is, it defines the angle at which the line crosses the x-axis.
Let’s return to our example:
y=2x+3
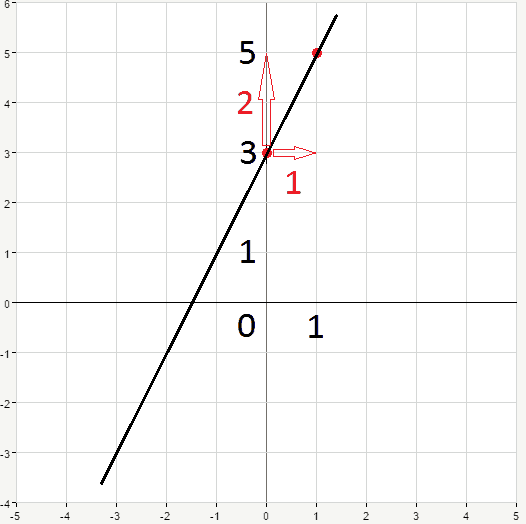
In this case y-intercept b=3 which means exactly that the line crosses y-axis at the point (0,3). The slope m=2=\frac{2}{1}. Number in the numerator stands for the change of y . Number in the denominator stands for the change of x. So we go 1 to the right and 2 upwards. And hence we have point (1.5):
By connecting two points we obtain our line. You may find it easier to memorize the formula for the slope the following way:
m=\frac{rise}{run}
where rise is how heigh the y rises, and run is how far the x runs. This is rise-over-run formula.
Once again, if you don’t want to deal with slopes and intercepts there is another way. For graphing a straight line it’s enough to know any two different points of this line. All you need to do is to pick two arbitrary values of x,then substitute them into the equation and find corresponding ys.
This is pretty much all you need to know about graphing a straight line on a plane. This or that way, lines are often present in algebra homework. Also you can face them in physics, for example, recall the case of motion with constant acceleration. The expression for velocity is the following:
v=v_0+at
where v_0 stands for initial velocity of the object, t is time of motion and a is acceleration. v-t graph in this case is a straight line with the slope a and y-intercept v_0.
Always keep in mind: asked to graph a line? two points and you’re done.



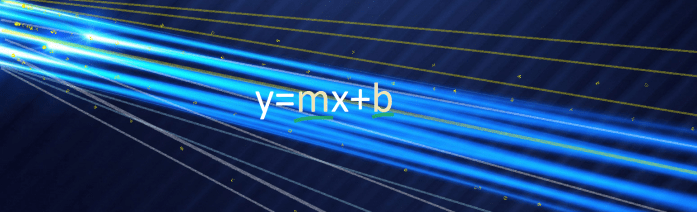



Very well! It’s always be very difficult for me to graph a straight line as I though maths is not my cup of tea. I always just got stuck in graphs or trigonometry but after reading this post I want to let you know you just taught me this in very easy way. A million of thanks for your team that gives their precious time and efforts for making helpful posts.
[…] words, let’s talk about solving a system of two linear equations. As we discussed earlier, a straight line on a plane is described by the following […]