In this section we’re going to discuss the most important properties of parabola, also we’ll show how to find its vertex, roots and intercepts. This information is needed to sketch the graph and also allows to analyze the behavior of given parabola. We’ve already shown how to sketch graphs of quadratic function, and now we’re going through most essential details. Let’s start with considering the equation of parabola. We already know how parabola looks like. Recall that graph of the parabola is U-shaped:
Equation of parabola is often written in the following way:
y(x)=ax^2+bx+c
This equation can represent any particular parabola, provided that we choose appropriate values of coefficients a,b,c. Say, to obtain the simplest parabola y=x^2 we should set a=1, b=c=0.
Parabola is a quadratic function. This means that the highest exponent of x must be two in our equation. You see coefficients a,b,c , which are certain numbers, they can be either natural or rational, or even irrational. They define the shape of our parabola. Let’s take a closer look at the equation and coefficients a,b,c and find out how the parabola depends on them.
Here’s video version of this tutorial:

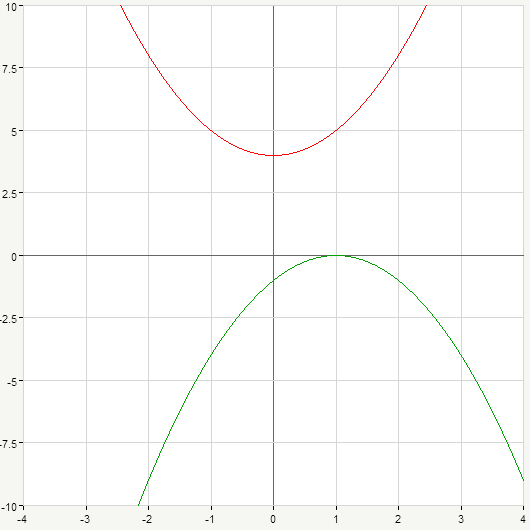
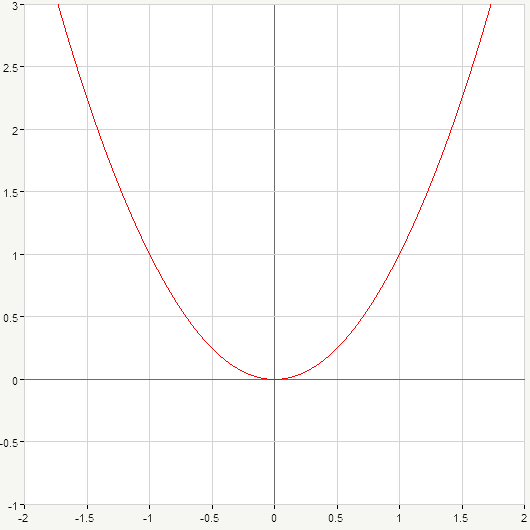
First, consider coefficient a beside the x squared in the equation. The sign of this parameter defines whether branches of given parabola are directed upwards or downwards. Parabola marked red on the picture below has a=1, while for green one it makes a=-1:
Remember that if a is positive then the parabola opens up. If a is negative branches of parabola are directed downwards. Here we should also say that a is supposed to be non zero because otherwise term with x^2 would disappear and we would obtain linear function y(x)=bx+c or simply a straight line. Thus, when doing homework with parabolas keep in mind that a \neq 1.
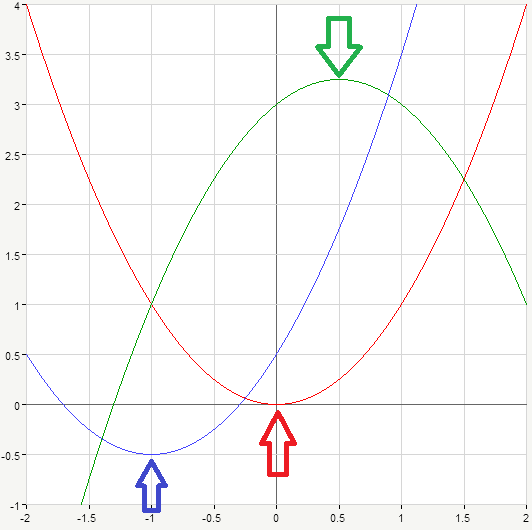
The coefficient a controls the speed of increase (or decrease) of the quadratic function from the vertex, greater absolute value of a makes the function change faster and the graph appears narrower. Smaller values of a lead to wider open graph. Consider parabolas y=x^2 (red curve), y=4x^2 (green) and y=0.5x^2 (blue):
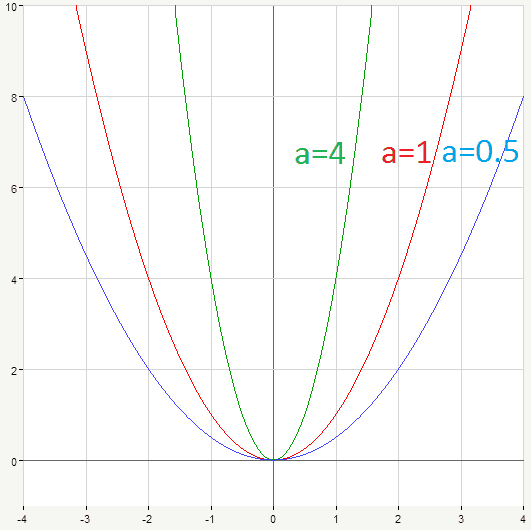
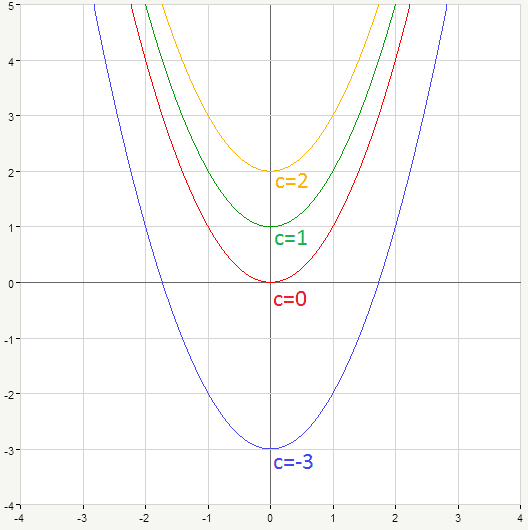
Now let’s talk about coefficient c, or so called free term (it doesn’t contain x). It defines y-intercept of given parabola graph. Indeed, if we substitute x=0 into the equation of parabola we’ll get:
y(0)=a\cdot 0+b \cdot 0+c=c
and it means that graph intercepts y-axis at the point x=0, y=c. Consider parabola y=x^2+c for several values of c coefficient:
So, roughly speaking, the c coefficient or, in other words, y-intercept defines how “high” parabola vertex is.
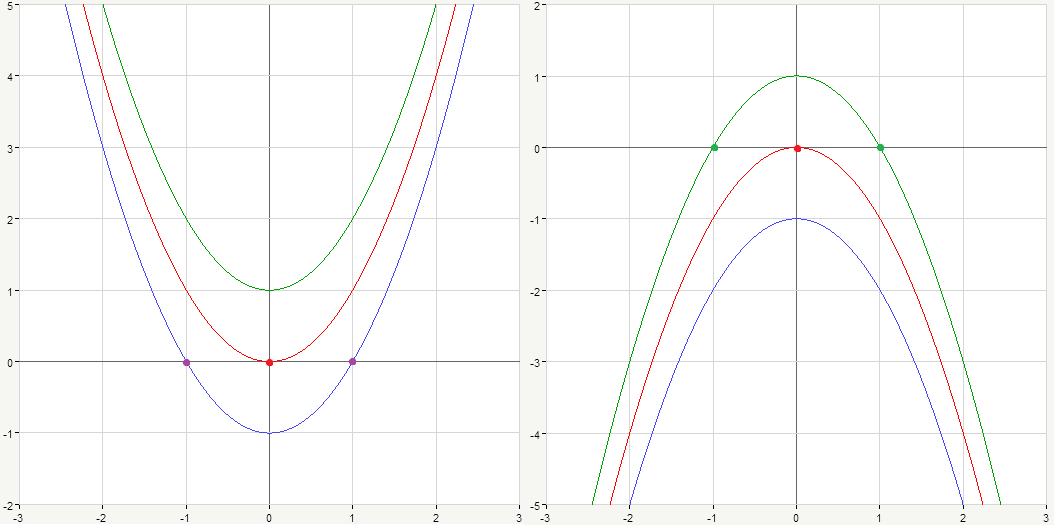
Let’s move on and discuss x-intercepts of the parabola. As you can see on the graph parabola can cross the x-axis in different ways. Basically, there are three possibilities: parabola either crosses the horizontal axis in two different points, or it touches the x-axis at one single point with ordinate y=0, or parabola is entirely above (or below) the x-axis.
To define exactly at what points given parabola crosses the x-axis we need to solve the equation y(x)= ax^2+bx+c=0 for x.
As you probably know, quadratic equation can have either two, or one, or no roots. These roots are the points of x-intercepts of parabola. In general, the roots of quadratic equation are defined by the following formula:
x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}
where $a, b, c$ are coefficients of the equation y(x)= ax^2+bx+c=0.
Expression D=b^2-4ac (staying under the square root in formula above) is called discriminant of quadratic equation. You can easily find out how many roots particular quadratic equation has by analyzing the value of the discriminant.
If D>0 there are two different roots because \sqrt D >0:
x_{1,2}=\frac{-b\pm \sqrt{D}}{2a}
If $D=0$ there is only one root because square root \sqrt D=0:
x=\frac{-b}{2a}
If D<0, given equation has no real roots because square root of negative number does not exist.
As we said before, graph of parabola is symmetric with respect to vertical y-axis. Recall y=x^2:
If we consider values x>0 and –x, corresponding values of y will be the same: y(x)=x^2, y(-x)=(-x)^2=x^2
In general case parabola’s axis of symmetry is parallel to the y-axis.
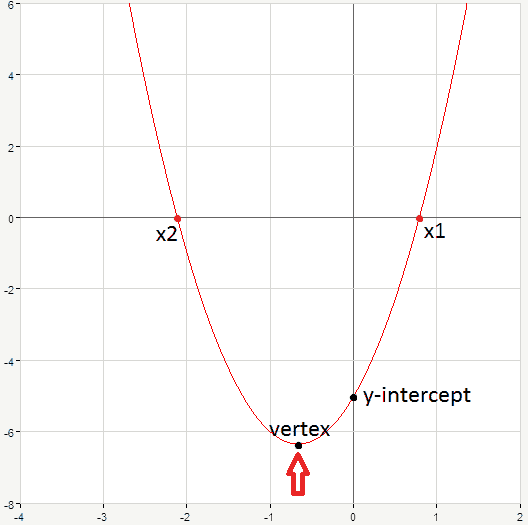
Also every parabola has a vertex , i.e. a point where it turns, hence it’s also called the turning point (shown by arrows at the picture below):
x-coordinate of vertex is defined as following:
x_0=-\frac{b}{2a}
At this point parabola achieves minimum if a>0 (the parabola opens upwards) and maximum if a<0 (it opens downwards). This becomes clear after sketching the graph. If your parabola looks like a cup the vertex is the point of minimum, otherwise parabola has maximum. So doing the sketch is helpful for better understanding.
To obtain the formula for vertex let’s modify our equation a bit. We’re trying to get a complete square:
\begin{aligned}y(x)&=ax^2+bx+c=a(x^2+\frac{b}{a}x+\frac{c}{a})=a(x^2+\frac{b}{a}x+(\frac{b}{2a})^2-(\frac{b}{2a})^2+\frac{c}{a})\\ &=a(x+\frac{b}{2a})^2+a(-(\frac{b}{2a})^2+\frac{c}{a})= a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a}\end{aligned}
The first term disappears if x=-\frac{b}{2a}. Suppose a>0. Then parabola achieves its minimum at x_0=-\frac{b}{2a} because we have constant term -\frac{b^2-4ac}{4a} and non-negative term a(x+\frac{b}{2a})^2. The latter is zero at the vertex and positive at all other points. Hence value of y is minimal at the vertex. Similarly, if a<0, parabola achieves its maximum at the vertex.
Axis of symmetry of the parabola is defined by the equation x=-\frac{b}{2a}. It’s a vertical straight line any point of which has x-coordinate defined by the formula x=-\frac{b}{2a}.
Example.
We’re given the following equation:
y=3x^2+4x-5
This equation is quadratic, therefore it represents a parabola.
First, we need to determine coefficients a, b, c: in our case they are a=3, b=4, c= – 5.
a=3>0, therefore the given parabola opens up.
c=-5 is the y-intercept of the given parabola.
Ok, now we need to find the roots of our equation. We start by calculating the determinant:
D=b^2-4ac=16-4\cdot 3 \cdot (-5)=76>0
This means that our parabola crosses the x-axis at two points. Let’s find their coordinates. Recall the formula defining roots of qudratic equation:
x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}
Substituting our coefficients we obtain:
x_{1,2}=\frac{-4\pm \sqrt{76}}{2\cdot 3}=\frac{-4\pm \sqrt{76}}{6}
x_1=\frac{-4+\sqrt{76}}{6}\approx 0.78
x_2=\frac{-4-\sqrt{76}}{6}\approx -2.12
Find the vertex of the parabola (as our parabola opens up, it will be the point of minimum):
x_0=-\frac{b}{2a}=-\frac{4}{6}=-\frac{2}{3}
To obtain y-coordinate of the vertex we need to substitute x_0 instead of x into the initial equation:
\begin{aligned}y_0 &=3x_0^2+4x_0-5=3(-\frac{2}{3})^2+4(-\frac{2}{3})-5=\frac{12}{9}-\frac{8}{3}-5=\frac{12-24-45}{9}\\&=-\frac{57}{9}=-\frac{19}{3} \end{aligned}
Now we have enough information to sketch the graph:
Summing up, we’ve discussed general equation of parabola and how its coefficients $a, c$ influence the graph. The third coefficient b will be considered in one of the next sections. Also we’ve talked about y- and x-intercepts and how to find them and we have obtained the formula for vertex of the parabola which is the point of maximum (or minimum, depending on the coefficient a). All this information can be useful for your algebra homework so it’s useful to memorize the formulas.







thanks a lot! love your blog