How to graph parabolas

What is a parabola? How to sketch its graph? These are the questions for this section. Sketching parabolas is commonly asked in algebra homework tasks, so some tips will be helpful. We’ll discuss the basic concepts and show you on simple examples how to deal with parabolas.

Let’s get started. In simple words, parabola is a U-shaped curve with some specific properties. However, note that not any U-shaped curve can be called parabola. It’s a common fact that math likes to describe everything by formulas. No surprises here, we also can write a formula for parabola. Basically, any parabola is described by some quadratic equation. 

Here’s video version of this tutorial:

This is the simplest parabola equation:

y=x^2

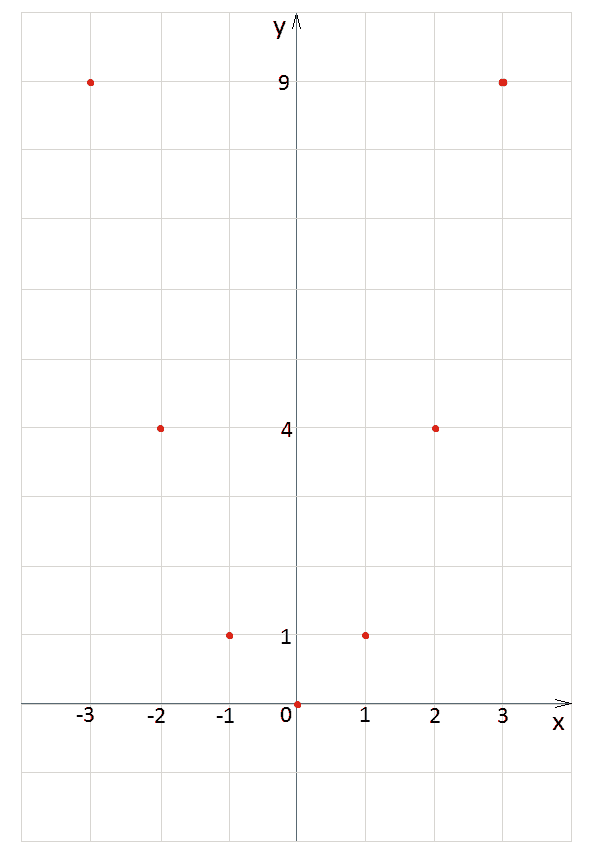
First let’s sketch it . For this we’ll need to fill in the table of values x,y. We simply take each value of x and substitute it into the equation to get corresponding value of y:

\begin{matrix} x&y\\ \\ {-3}&9\\-2&4 \\-1&1 \\0&0 \\1&1\\2&4\\3&9\end{matrix}

Now we can mark all the points on coordinate plane:

Finally, we sketch our parabola by connecting points. We draw a smooth curve going through each of seven points. At this point you can ask, “Nice, but how did you do this? Why don’t we just make it a polyline?” If you calculate more points you’ll see that it’s indeed correct, parabola has no angles or something.

Look closer on the values in our table and onto the obtained graph. Do notice symmetry in there! For example,  for x=-3 and x=3 the corresponding values of y are the same: y=9. For x=1 and x=-1 we have y=1.

Let’s change our equation a little bit and make it y=x^2+2. Obviously, we need new table of values:

\begin{matrix} x&y \\ \\ {-3}&11\\-2&6 \\-1&3 \\0&2 \\1&3\\2&6\\3&11\end{matrix}

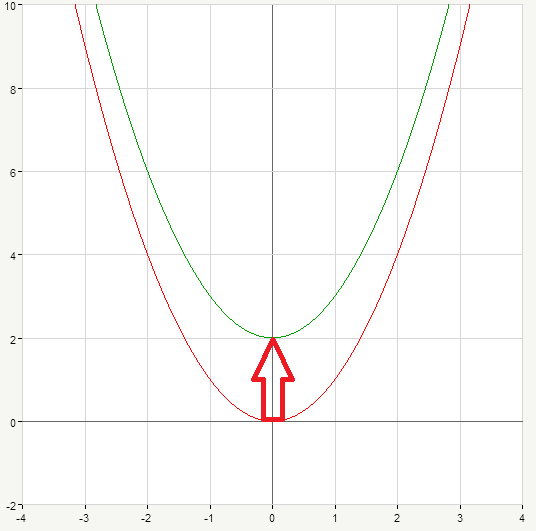
Now we can connect points and get a new parabola. New graph (marked in green) simply goes higher than initial y=x^2 (marked in red), its shape is the same, our graph is just shifted up for 2 units.

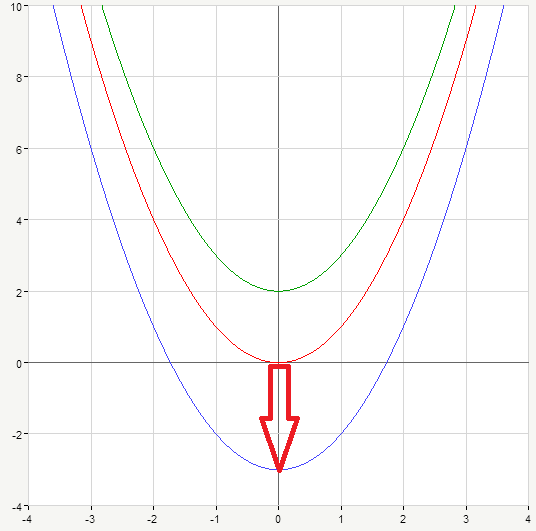
The situation is the same, if we have y=x^2-3 . Once again, we start with doing necessary calculations:

\begin{matrix} x&y\\ \\ {-3}&6\\-2&1 \\-1&-2 \\0&-3 \\1&-2\\2&1\\3&6\end{matrix}

Now the parabola moves down for 3 units (blue curve on the picture below):

Thus, if you add some number (like we did with 2,-3) to the right part of the equation y=x^2, your new graph will just shift up (if the added number is positive) or down (if it’s negative).

Ok, let’s go another way. Again, our initial function is y=x^2. Consider y=2x^2, so we multiply every value of  y=x^2 by 2 to obtain our new equation. We need to find new values of y:

\begin{matrix} x&y\\ \\ {-3}&18\\-2&8 \\-1&2 \\0&0 \\1&2\\2&8\\3&18\end{matrix}

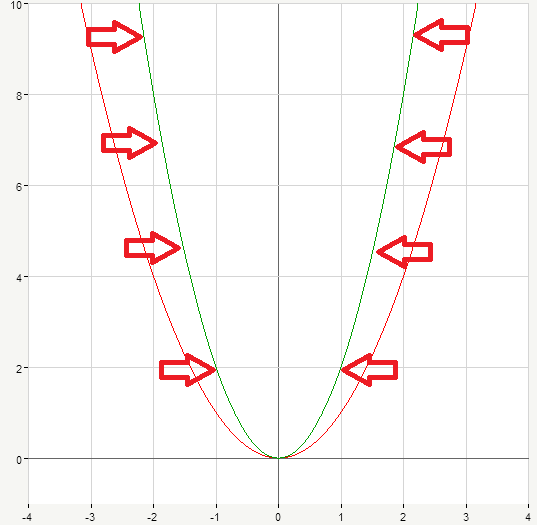
We have updated our graph (marked in green on the picture, initial graph is represented by red curve), this time it’s squeezed to the y-axis. Also we can notice that it’s stretched in vertical direction:

Of course, we can multiply x^2 by any other number, for example let’s consider y=4x^2. Again, we fill in a new table of values:

\begin{matrix} x&y\\ \\ {-3}&36\\-2&16 \\-1&4 \\0&0 \\1&4\\2&16\\3&36\end{matrix}

Our new graph (blue curve on the picture below) is narrower then previous (green) one:

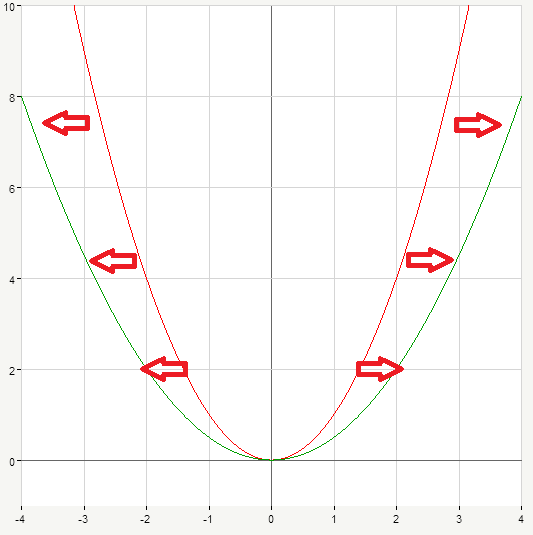
Here we used positive numbers (namely 2,4) as multipliers for initial expression x^2. Let’s take a look at one more example. Suppose y=-x^2, i.e. we multiply every value of y=x^2  by -1. Again, we need to fill in the table for x,y:

\begin{matrix} x&y\\ \\ {-3}&-9\\-2&-4 \\-1&-1 \\0&0 \\1&-1\\2&-4\\3&-9\end{matrix}

In this case all the values of y are negative. We obtained parabola and it looks like it’s inverted, the branches are directed downwards:

Generally, if you pick negative number (like we did with -1) you’ll get parabola opening downwards.  If you pick positive number your parabola will open up, its branches will be directed upwards, like our initial y=x^2.

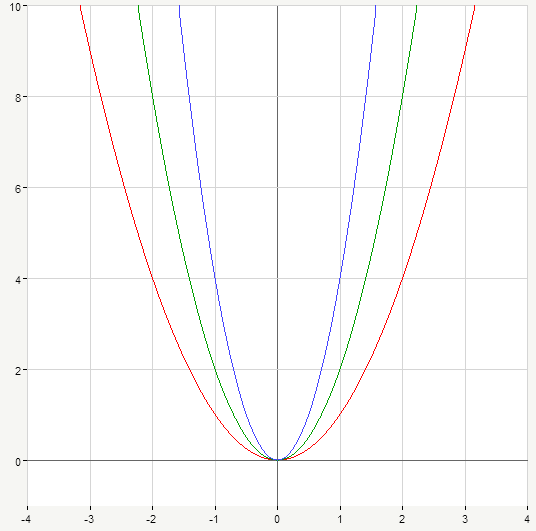
Let’s see what will happen if we multiply x^2 by \frac{1}{2}, so our parabola’s equation takes the form y=\frac{1}{2} x^2. Graph of y=x^2 is marked in red, new graph y=\frac{1}{2} x^2 goes in green:

The graph is widened in comparison to our initial parabola. Let’s consider one more example, suppose y=\frac{1}{4} x^2. On the picture below it’s marked in blue:

Notice that \frac{1}{4}x^2 provides even wider graph than \frac{1}{2}x^2.

Thus, the greater positive number you use to multiply the right part of parabola equation y=x^2 the narrower your new graph is. And inversely, the smaller number you take the wider graph you will obtain.

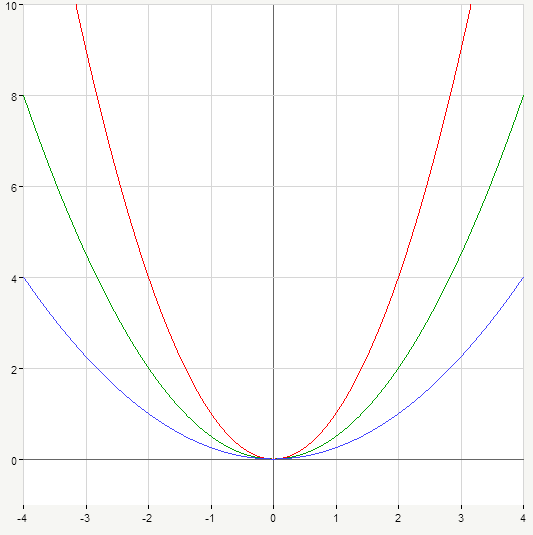
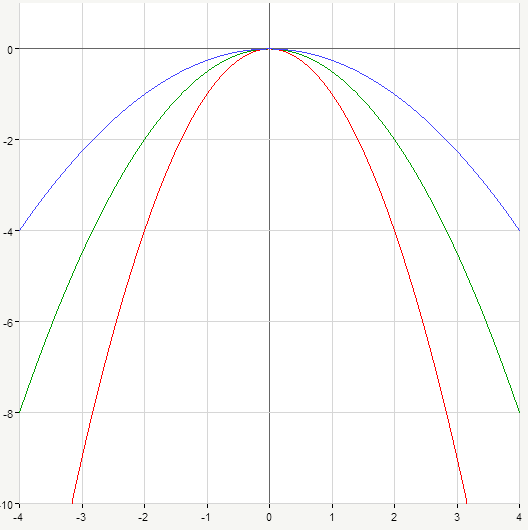
This works just the same for negative numbers, of course. The only difference is that in such case branches of parabolas will be directed downwards. Below are the graphs of y=-x^2 (red curve), y=-\frac{1}{2}x^2 (green), y=-\frac{1}{4}x^2 (blue):

Hopefully, you are getting familiar with parabolas now and won’t be stuck when facing them in your math homework. We’ve considered some examples of what a parabola can be. Generally, if you have some equation where you have y and some terms with x, provided that the greatest exponent of x is 2, then  it’s parabola. For example, y=x^2-2x+3 is a parabola because we have here x^2 and –2x so the greatest exponent of x is square.

Parabolas also can be a bit more complicated, like y=(x-2)^2+2. In fact, it only looks trickier, yet we simply open the braces and  get y=x^2-4x+4+2. In this form we have our x^2 and can certainly say we’re dealing with a parabola. We’ve sketched graphs of parabolas by filling the table of values, which means we solved the equation (for example, y=x^2) for y. In other words, we set certain values of x (namely, x=-3,-2,-1,0,1,2,3) and found corresponding values of y by substituting into the equation. In such case y is called the function of x because you can find y through the equation for each value of x . It’s usually denoted as y=f(x). In our case y=f(x)=x^2 and it’s called parabola equation as you already know.