Do you think this is just a bunch of meaningless numbers or something more? 9 \: 27 \: 12 \: 15 \: 22 \: 5 \: 27 \: 19 \: 3 \: 9 \: 5 \: 14 \: 3 \: 5 Later we’ll give you the answer. But before let’s talk about cryptography. Do you know what’s that? We’ll start with a bit of history. Cryptography is the science of secret writing. Its name comes from the Greek words Kryptos, meaning hidden, and graphene, which means writing. By the way, there is also steganography – the science and art of writing hidden messages. Don’t mix them up, though. Steganography and cryptography are not the same. Cryptography is the science of codes and ciphers. Steganography is the science of secure data transmission through the secrecy of the very fact of the transfer. 
Code is just a pre-arranged word or sentence. Foreign languages are somewhat similar to the secret codes, for example, the word “hello” in Spanish is written as “hola”. Most codes have a dictionary for encryption – decryption just like human languages. People started to use ciphered texts in ancient time. Julius Caesar used a simple alphabet substitution, shifting to 3 letters. For example, taking the word “help”, you move it down 3 letters of the alphabet, getting “jgnr”. For a while it worked, yet soon too many people learnt to read and decipher this code so it got obsolete. One of the weaknesses of such methods is low resistance to frequency analysis. For example, knowing the regular frequency of the letters in the text in particular language, you can find a match between the characters and the message in the code. To reduce the risk of disclosure for the algorithm, new methods using a proportional change have been developed. 
In such approach a single letter is replaced by several characters. Their number is proportional to the frequency of occurrence of letters in the message. Below you can see a table with frequency of each letter in sample text. 
Ok, now let’s take a look at our example. Here’s the sequence we’ve started with: 9 \: 27 \: 12 \: 15 \: 22 \: 5 \: 27 \: 19 \: 3 \: 9 \: 5 \: 14 \: 3 \: 5 Apparently, this is an encrypted message. Let’s simply replace each letter of the alphabet by its serial number from 1 to 26. We’ll obtain the following code table: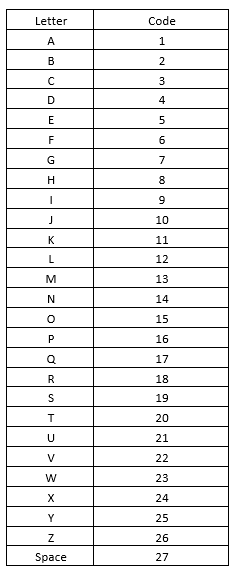 
Decoding our message (i.e. replacing each number by corresponding letter), we obtain the following: I \: LOVE \: SCIENCE As we can see our example is simple but it’s a start. It should also be said that, despite the development of deciphering methods there are still intractable cryptanalyst letters. For example, the hieroglyphic inscriptions on the Phaistos disk, presumably belonging to the Minoan civilization on Crete. 
Or another one, Voynich’s manuscript, is an example of an encrypted message, the manuscript is over 400 years old. It consists of 240 pages with illustrations of unknown plants, herbal recipes, astrological charts, human figures and inscriptions in an unknown language. 
Today, cryptography continues working on deciphering the manuscript. One of the mysteries of modern cryptography is “Kryptos”. 
It is a sculpture created by artist James Sanborn (James Sanborn), and installed in the office of the CIA in Langley, Virginia. Sculpture is an encrypted text, divided into four sections. Since its opening in 1990, experts have been trying to decipher the inscriptions, but so far they have coped with only three sections. The last part of the code of this sculpture is not decoded. Thus, at all times for the transmission of classified information, people used ciphers. And today, with the advent of the Internet, where banks and government organizations store their encrypted secrets, this industry is evolving even more rapidly. At the moment, there are still codes that cannot be decoded even by the best experts in cryptography.
0 Comments
