A series is an infinite addition of an ordered set of terms. The infinite series often contain an infinite number of terms and its nth term represents the nth term of a sequence. A series contain terms whose order matters a lot. If the terms of a rather conditionally convergent series are suitably arranged, the series may be made to converge to any desirable value or even to diverge according to the Riemann series theorem. Let the terms in a series be denoted by the symbol, an , and the nth partial summation be denoted using the following sigma notation for any natural number n:
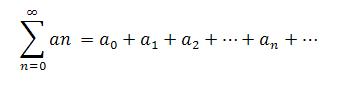
Types of Series
1. Harmonic Series: This is an example of divergent series.

Harmonic series is divergent because its sequence of partial sums is rather unbounded.
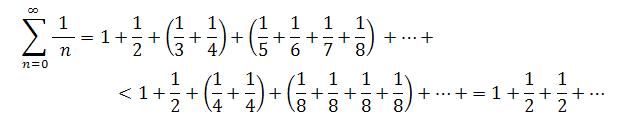
Thus
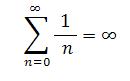
However, the alternative harmonic series converges to the natural logarithm of 2.
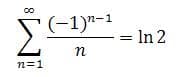
2. Geometric Series: Geometric Series is a series where the ratio of each two consecutive terms is a constant function of the summation index.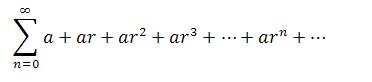
A geometric series may converge or diverge depending on the value of the common ratio. If the common ratio is greater than or equal to 1, the series diverges while if the value of the common ratio is between 0 and 1, it converges and the sum is given by:
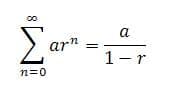
3. P-Series: P-series is a series where the common exponent p is a positive real constant number.
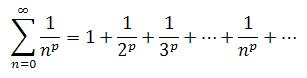
The P-series diverges if the common exponent is less than or equal to 1 which is in sharp comparison with the harmonic series. The series converges if the common ratio is clearly greater than 1; though the value of the sum at this point is only known in a few instances. For p=2 which is the sum of the inverses of the squares, the sum is (p^2)/6.
4. Alternating Series: An alternating series is a series in which the terms alternate in sign.
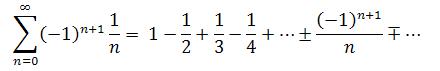
Such series will only converge if and only if its terms decrease in absolute value with respect to zero as a limit.
5. Power Series: A power series has each term as a distinct constant.
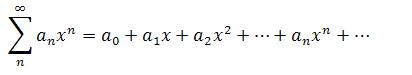
Such series would either converge when the value of x equals zero or for all real values of x, or for all real values of x given that –R<x<R. The radius of convergence is the interval with the values (-R, R).
Tests for Convergence of a Series
The test of convergence of a series follows a series of measures. When the sequence of partial sums of a series converges, the series converges. However, a series converges absolutely if the series continue to converge when the absolute values of all its terms have been taken, that is, all values have become non-negative. A series is said to converge conditionally if it does not converge absolutely though it converges.
If a series does not converge, then it diverges. For the term series, the series diverges if the limit of the sequence of it terms is not zero – this is really not a test for convergence and must be used with care.
Test of convergence for two non-negative series:
If two series are such that for all values of n where 0 less than or equal to which is also equal to or less than . If the first series diverges, the second does diverge. The reverse is the case so that if the second series converges, the first one does converge.
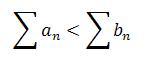
Limit of comparison test: There is, however, a limit to the comparison test for the two non-negative series. If the limit exists and it is finite, a real number greater than zero, then both series converge or both series actually diverge.

Integral Test: For a series whose terms are positive but decreasing, then the series and its integral,
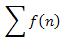 |
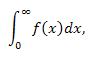 |
either both converge or both diverge.
The ratio test of convergence of series: If a series has positive terms and if its limit exists, then the series converges if the result of the limit is less than 1 and diverges if this result is greater than 1.

However, if the result is 1, then the test is inconclusive.
The root test of convergence of series: If a series has positive terms and if its limit exists, then the series converges if the value of its limit is less than 1 and diverges if this value is greater than 1. If the value of the limit equals 1, then the test is inconclusive.




