The objects commonly referred to as platonic solids are regular solids or better still, they are called regular polyhedra. The solids are convex polyhedra that have equivalent faces made up of regular polygons that are congruent-the word polyhedra means ‘’many faces’’ in Greek. There are exactly five of the platonic solids called polyhedra and they are:
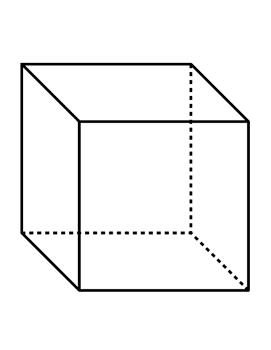
| The Cube
|
The cube is a polyhedron that has six square faces, eight vertices, and twelve edges |
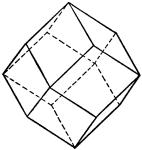
| The Dodecahedron
|
The dodecahedron is a polyhedron that has twelve pentagonal faces, twenty vertices, and thirty edges.
|
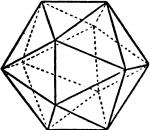
| The Icosahedron
|
The icosahedron is a polyhedron with twenty triangular faces, twelve vertices, and thirty edges.
|
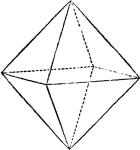
| The Octahedron
|
The octahedron is a polyhedron with eight triangular faces, six vertices, and twelve edges.
|
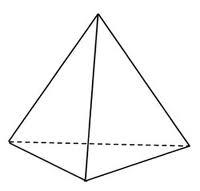
| The Tetrahedron
|
The tetrahedron is a polyhedron that has four triangular faces, four vertices, and six edges.
|
Euclid proved the existence of these five platonic solids in a proposition of the elements. These solids are also often referred to as ‘’cosmic figures’’ according to a publication made by Cromwell in 1997 though Coxeter had used this term to collectively refer to both platonic solids and Kepler –Poinsot solids.
Arguments in support of the existence of five platonic solids: We may naturally wonder why there should be just five platonic solids in existence in the universe and also imagine if there might be some others not yet discovered. It has, however, been shown that there must be five and not more than five of these solids.
The first attempt at showing that there could be just five platonic solids comes from the following thinking: At each vertex or point of an object, three faces must necessarily come together. This is because if just two came together, the reasoning shows that the two will collapse against each other so that no solid could be formed.
The second thinking came from the observation that the sum of the interior angles of the faces meeting at each vertex must be less than 3600. This is because if the otherwise position holds, we shouldn’t expect the vertices to fit together.
Fitting three, four, or five equilateral triangles together to form tetrahedron, octahedron, and the icosahedron: Now, the interior angle of any equilateral triangle is 600. It follows then that we could bring together three, or four, or five of such faces at a vertex and then obtain the tetrahedron, the octahedron, and the icosahedron. Recall that icosahedron has twenty triangular faces, twelve vertices, and thirty edges while octahedron has eight triangular faces, six vertices, and twelve edges; and tetrahedron is a polyhedron that has four triangular faces, four vertices, and six edges.
How squares can add up to a cube: For a square, each interior angle is 900, so that we can only fix three square faces together at the vertex in order to obtain a cube (Note that if you fix four squares together you would not obtain a solid but a tessellation). Recall that a cube has six square faces, eight vertices, and twelve edges.
The making of dodecahedron from regular pentagon: Using the regular pentagon, each interior angle is 1080, so that we can only fit three together to give us the dodecahedron which has twelve pentagonal faces, twenty vertices, and thirty edges.
What we have from this illustration is five regular polyhedra. It is therefore true that we can only have five polyhedra and not more at all. However, you might think of fitting three regular hexagon together since each has an interior angle of 1200, and the sum of three angles give 3600, but combining three regular hexagons would not give a polyhedra because the vertex angle will be just be 3600 which is flat and not a solid. The same argument goes for any other combination other than the ones that make up the five polyhedra platonic solids.
The Greek Philosophers’ thought of the platonic solids: The Greeks who were known to be very inclined to mathematics to the point they accepted it like religious truth found in platonic solids a reason to propound issues of thought. In the same vein, Plato considered these solids as building blocks that are fundamental, something like the atom of nature and therefore assigned to them the essential elements of the universe. Plato therefore toed the line of Empedocles by assigning fire to tetrahedron, earth to the cube, air to the octahedron, water to the icosahedron, and element cosmos to dodecahedron. The dodecahedron particularly exited Plato and therefore, he felt since it was so different from others with its pentagonal faces, it does implies that the stars and planets are made of it.
This may look as an idea that we are not familiar with or even totally naïve but the truth is that Plato’s thought were full of useful ideas which also brought out real knowledge. A good example here was the work of Johannes Kepler who had used the idea of platonic solids to assume that the distances of orbits were circular but from the work of Tycho Brahe, which he inherited; Kepler was able to understand better that the planets moved round the sun in ellipses and not circles. This discovery was later used by Isaac Newton not too long after to propound his law of universal gravitation which governs the motion of planets and it is the basis of our modern idea about the universe.
It is to be noted that the interest and beauty of platonic solids continue to stir and inspire all categories of people and not only mathematicians.