Taking a calculus class, you’ll surely be asked to find derivatives of functions. Sometimes it’s not that easy to do. If your function is not among common ones, you need to apply special rules to find its derivative: product rule, quotient rule, chain rule, etc. In this section we’re going to show you an example of using chain rule. Suppose we need to find the first derivative of the following function:
h(x)=(2x^2+3)^{10}
In fact, in this particular case, we can just open the braces using binomial theorem and obtain a polynomial, derivative of which is easily found due to table of derivatives. But not that fast, we have 10th power and opening the braces would be a troublesome business. So let’s try to use chain rule instead, you’ll appreciate simplification it suggests.
Let’s follow the chain rule algorithm we described before. Recall it:
1. Name inside and outside function.
2. Find derivative of the outside function due to table of derivatives using the whole enclosed expression as an argument.
3. Proceed if there’s more than one outside function.
4. Find derivative of the inside function. This time the argument is simply “x” (or some other symbol due to initial denotation).
5. Substitute all the derivatives into the formula for chain rule.
Simply follow the chain:
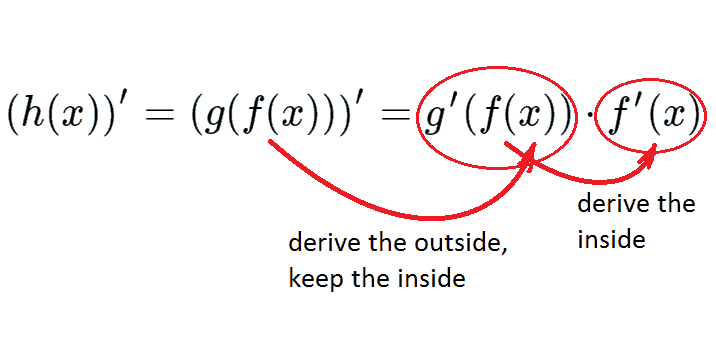
So, firstly we need to determine what function is inside and what is outside. Let’s try to imaginary calculate y(1). Obviously, at first we calculate 2\cdot 1+3=5 and then 5^{10} so the polynomial 2x^2+3 is an inside function and power (2x^2+3)^10 is outside. Thus, we obtain:
g(f)=f^{10} – outside function
f(x)=2x^2+3 – inside function
This way our initial function is represented as h(x)=g(f(x)).
Check video version of this tutorial:
Move on to the second step. Let’s find derivative of the outside function. We know that (x^{10})’=10x^9. In our case instead of x we put in 2x^2+3. So the derivative of the outside function is g'(f)=10(2x^2+3)^9.
The third step: we need to find derivative of the inside function. As we’re dealing with a polynomial, we can write it down right away: f'(x)=(2x^2+3)’=4x.
Finally, we’ve found all the needed stuff. Due to chain rule we obtain the derivative of our initial function:
h’=((2x^2+3)^{10})’=10(2x^2+3)^9\cdot 4x=40x(2x^2+3)^9
And that’s it. Needless to say, without chain rule you’d be still calculating the coefficients in binomial formula. This is not such a big deal, though. However, note that in contrast to this example, chain rule is sometimes the only option, so be attentive. Also be ready to use several rules simultaneously, if your particular homework implies this. For example, imagine a function which itself is a product of two composite functions. In such case, you won’t get away with chain rule alone. We’ll demonstrate such examples in our next section.
And you can! Do math!
