Do you know what is a determinant? A determinant of a matrix is a special number which is defined only for square matrix. It can be calculated in several ways, today we’ll introduce one of them which is called Laplace expansion.
Why do we need determinants? Basically, the determinant can tell us a lot of useful things about matrix, it’s helpful when finding the inverse matrix and solving systems of linear equations (recall Cramer’s rule) and so on.
Let’s find the determinant of the given matrix:
A=\begin{pmatrix}1 & {-1} & 0 & 2 \\3 & 1 & 4 & 1 \\0 &0 & 1& -3\\1& -1& 0 & 4\end{pmatrix}
Check our video version of this tutorial:

First of all, matrix should be square to have a determinant. Keep that in mind while solving your math homework with matrices. If the matrix is not square determinant for it does not exist! Our matrix is 4×4, it’s a square matrix of size 4 so it’s all right and we can calculate the determinant.
Recall that there’s nice rule for calculating determinants (of any size!) which is described by the formula
\Delta =\sum_{i,j=1}^{n}(-1)^{i+j}a_{ij}M_{ij}
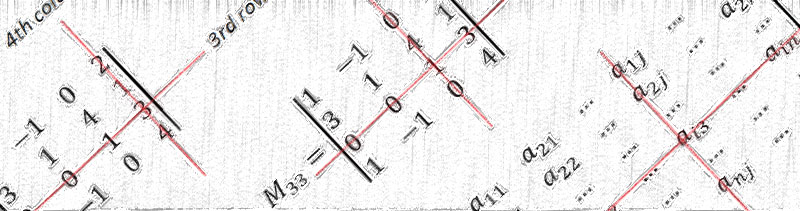
where Mij is minor for ij entry of matrix A. Mij is a determinant of the matrix which is obtained of initial matrix A by crossing out i-th row and j-th column:
Rule represented by the formula we’ve considered suggests that we set to constant one of indices i or j . The index which is not constant changes from 1 to n (in our case from 1 to 4 because initial matrix A is of size 4×4). Practically, we need to choose particular row or column of the matrix and write down the sum using entries of the chosen row or column.
As you can see, each addend is a product of some entry by its minor and the term (-1)i+j. The last factor contributes only plus or minus sign because, as we already said, it’s equal to either 1 or (-1). So for convenience we ought to pick up the row or column which contains zeros or small numbers if possible. Let’s chose the third row because it contains two zeros. It means that we set i=3. The second index j is changing from 1 to 4:
\begin{aligned} \Delta &=\sum_{j=1}^{4}(-1)^{3+j}a_{3j}M_{3j}\\ &=(-1)^{3+1}a_{31}M_{31}+(-1)^{3+2}a_{32}M_{32}+(-1)^{3+3}a_{33}M_{33}+(-1)^{3+4}a_{34}M_{34} \end{aligned}
We see that
a_{31}=a_{32}=0
Therefore:
\begin{aligned}\Delta& =(-1)^{3+1}\cdot 0 \cdot M_{31}+(-1)^{3+2}\cdot 0 \cdot M_{32}+(-1)^{6}a_{33}M_{33}+(-1)^{7}a_{34}M_{34}\\&=a_{33}M_{33}-a_{34}M_{34}\end{aligned}
From the last formula it’s clear that to find the determinant of initial matrix A we just need to calculate M33 and M34 .
Let’s calculate them using rule of triangles (because these determinants are of size 3×3). Note that we could use the approch of the first part of our calculation for calculating these determinants as well.
After writing down the expansion by the third row we obtain the following:
\begin{aligned} M_{33}&=1 \cdot \begin{vmatrix}1&-1 &2 \\3& 1 &1 \\1&-1 &4\end{vmatrix}=1\cdot1\cdot4-1\cdot1\cdot1-1\cdot3\cdot2-(2\cdot1\cdot1-1\cdot3\cdot4-1\cdot1\cdot1)\\&=4-1-6-2+12+1=8\end{aligned}
\begin{aligned} M_{34}&=1 \cdot \begin{vmatrix}1&-1 &0 \\3& 1 &4 \\1&-1 &0\end{vmatrix}=1\cdot1\cdot0-1\cdot1\cdot4-1\cdot3\cdot0-(0\cdot1\cdot1-1\cdot4\cdot1-1\cdot3\cdot0)\\&=0-4-0-0+4+0=0\end{aligned}
By the way, the last determinant we could immediately say zero because it has two equal rows (it means that corresponding matrix is degenerate and its determinant is zero). Generally, when matrix has either pair of equal rows (or columns) or one row(column) is a linear combination of several other rows(columns) then determinant of such matrix equals zero.
Therefore, we obtain the following:
\det A=a_{33} M_{33}-a_{34} M_{34}=1\cdot8+3\cdot0=8
\det A=8
That’s our answer.
Of course, if we’d choose another row or column of A to write the formula it would not change the answer. It’s just the matter of convenience.




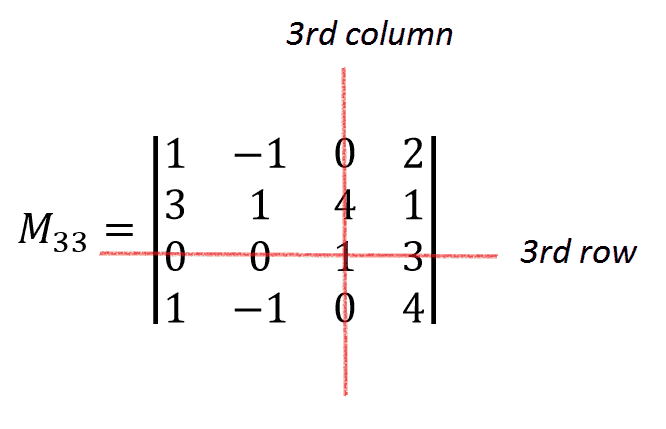
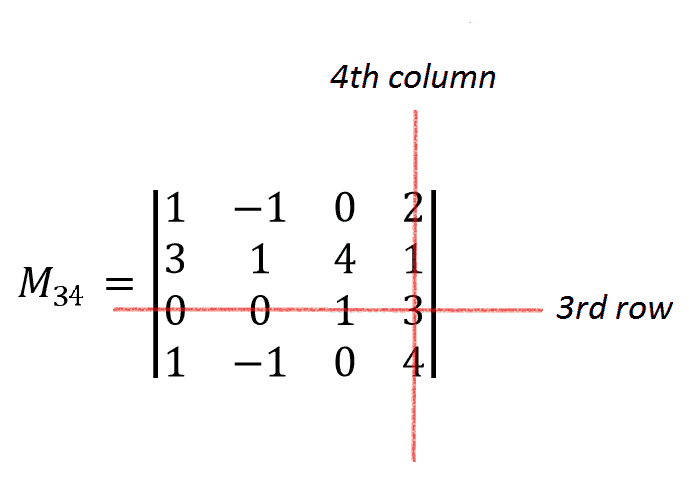


[…] me, please! I’m stuck..” This is the second part of our tutorial explaining how to calculate determinants. We’re asked to calculate the determinant of the following 4×4 […]
[…] is called minor of matrix A and is a determinant of matrix obtained by removing row “i” and column “j” from initial matrix […]
[…] elimination can be performed comparatively easy for systems of order higher than, say, 4 when calculating determinants gets […]