Logarithms – that is how usually the “inverse” of exponentials are called (just as division is the opposite of multiplication and subtraction is the opposite of addition). Logarithms “undo” exponentials.
y = bx is equivalent to logby =x
Above we can see the exponential statement “y = bx“. Then goes the equivalent logarithmic statement “logb(y) = x”. It is pronounced “log-base-b of y equals x”. The “the base of the logarithm” is the value of the subscripted “b”. In an exponential the base b is not equal to 1 and is always positive just like the base b for a logarithm is not equal to 1 and is always positive. No matter what may be aside, the logarithm is usually called the log “argument”. You should make a note of the fact that the base in the log equation and the exponential equation is “b”. Moreover, when one switches between the two equations, the y and x switch sides.
You may see the expressions which looks like this: “log4(7)”. This expression means that “the power which turns 4 into 7 when put on 4”. And that’s what they have done (put it on 4), which technically means that they have turned 4 into 7.
To cut the long story short, here are the things you have to get from this lesson:
- Logarithms are really exponents (powers); they’re just written differently.
- The Relationship: “logb(x) = y” means the same thing as “b y = x”.
- logb(a) is undefined if a is negative.
- logb(bn) = n, for any base b.
- logb(b) = 1, for any base b, because b1 = b.
- logb(0) is undefined for any base b.
- logb(1) = 0, for any base b, because b0 = 1.
Any positive value may serve as the base of a logarithm. But the point is that 2 log bases can be more useful than the rest. The base – 10 (“common”) log is very popular. This popularity was established historically and usually it is written as “log(x)”. For instance, both the Richter scale (earthquake intensity measure) and pH (substance’s acidity or alkalinity measure) involve base-10 logs. If there is not written log base, you have to assume that the base may be 10 (in algebra classes).
There’s one more log which is of a great importance too. It is called “natural” (base-e) log. It is denoted as “ln(x)”, which one should pronounce as “ell-enn-of-x”. In the sciences and in math the number e arises and so does the natural log. That is why you have be well-familiar with it.
The logarithm graph is similar to the graph of the square root:
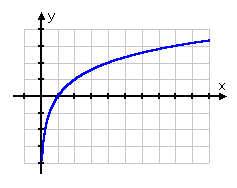
But the graph of square root stops at the point (0, 0) and the graph of the logarithm never passes through the origin. It passes through (1, 0). Then the graph goes down along the right-hand y-axis side. As we know, the log function is the exponential function inverse, the log graph is the exponential graph flip.
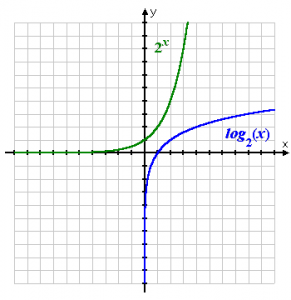
The exponential goes along the x-axis top. Then, at the point (0, 1) it is crossing the y-axis. After that it shoots up. The logarithm is riding up the y-axis right side, then (at the point (1, 0) it is crossing the x-axis and at the end it is shooting right.




