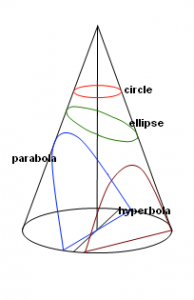
In general, conic sections represent the curves obtained from intersecting by a plane some “double-napped” cone (it’s like two cones were put “nose to nose”, perfectly balancing). The term “sections” is used with the same meaning as in science or medicine. In these areas, a little sample (obtained from a biopsy for example) is frozen and then very thin and little slices (they are also called “sections”) are taken to have a view of them under a microscope. When we’re talking about conic sections, we mean what follows when the cones are sectioned at different angles.
We intend to pay our attention to: how to find curves, points and various details of their graphs. Moreover, we will devote our explanation to the solving and setting up conics equations in order to work out different classic word problems.
To get familiar with this topic, you have to be aware of the following basic terms: focus, center, axis, vertex, major axis, minor axis, directrix, and locus.
Usually, in such cases, the basic question comes up, “Given an equation, how can I find out what conic sort it is?” There’s a “typical” equation form for each conic:
Parabola: Ax2 + Dx + Ey = 0
Circle: x2 + y2 + Dx + Ey + F = 0
Ellipse: Ax2 + Cy2 + Dx + Ey + F = 0
Hyperbola: Ax2 – Cy2 + Dx + Ey + F = 0
You can rearrange these equations in many different ways. There’s a special form for each conic you have to learn and be able to recognize. Also there are some equations characteristics that never change for every sort of conic. If you remember all these characteristics, you may look through a short check-list in order to find out what type of conic you deal with.
If you are provided with the general-form conic equation in the following form Ax2 + Cy2 + Dx + Ey + F = 0, or if you have rearranged in order to put the equation in this form, you should create a chain of logical thoughts in your mind. You should check whether both variables squared: if yes have to proceed to the next test, and if not it is definitely parabola. The next step is to look on the signs of the squared terms. If they have contrary signs, it is definitely hyperbola, if not, we move to the next test. If the squared terms are multiplied by the same number, it is definitely a circle, if not – this is an ellipse.
If your equation has variables at each its side, you have to rearrange the terms (in your mind or on the piece of paper) in order to put on one side the squared things together.
The graphs of conic shapes could be either parallel the y-axis or x-axis, either “slanted” like on the following figures:
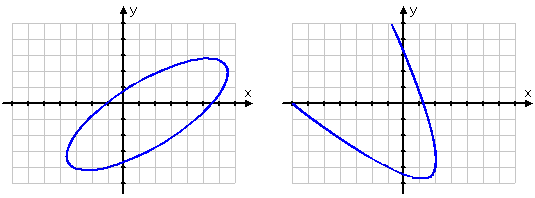
The equations of such conics become messy and you have the use some trigonometry. If you are interesting why B is absent among the coefficients in the “general conic” equation, for instance, Ax2 + Cy2 + Dx + Ey + F = 0, you have to know that the coefficient B should be placed at “xy” term to describe “slanty” conics.




