Johannes Kepler, a German mathematician and astronomer who lived between 1571 and 1630 was a determined scientist who was so interested in studying the motion of planets such that he started to demonstrate early in his career that the planets were always in circular motion in agreement with the Aristotelian credence using Platonic solids to describe the motion of the planets.
Kepler inherited the works of Tycho Brahe, a Danish astronomer who died in 1601and to whom Kepler was a friend and assistant. Kepler studied Tycho’s works and data without a telescope; he came to understand many things about the planets and their motions particularly that if focus could shift from seeing the earth as the centre of the universe to the sun being the centre, then he concluded that the motion of the planets must then be seen as elliptical.
Upon the basis of his proposition, Kepler propounded three laws that are being regarded as Kepler’s laws of planetary motion. The laws are stated as follows:
1. Kepler’s first law of planetary motion states that the orbit of each planet is an ellipse with the sun at one focus.
2. Kepler’s second law of planetary motion sates that the line segment joining a planet to the sun sweeps out equal areas in equal time intervals (this law is often called the law of equal areas).
3. Kepler’s third law of planetary motion states that the square of the period of revolution of a planet about the sun is proportional to the cube of the semi-major axis of the planet’s elliptical orbit (the law is often referred to as Kepler’s law of periods).
The following diagrams illustrate Kepler’s laws of planetary motion vividly.
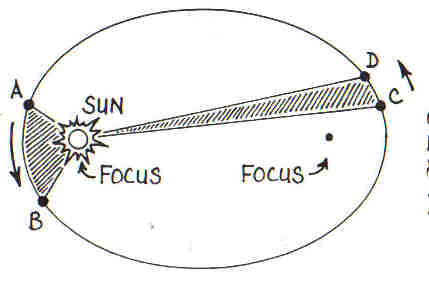
Kepler’s laws shows that the speed with which a planet revolve around the sun is not uniform but rather changes periodically. The speed is fastest when the distance of the planet from the sun is the shortest which is referred to as perihelion while the speed is slowest when the planet is farthest away from the sun which is referred to as aphelion. It is good to remember that the a circle is an ellipse with its eccentricity as zero and its foci coincide in the centre of the circle but the planets are not really circles, they are ellipses with their eccentricity not equal to zero.
Kepler’s third law implies that the quantity, Y2/a3, is the same for every planet no matter what the planet is in the solar system if Y is taken as the length of the planet’s year which is the time the planet takes to make a complete revolution round the sun and the length of the semi-major axis of the planet’s orbit is denoted with a. The inference from this is that if the orbit of a planet is known, the length of the planet’s year can be determined.
Kepler’s laws were deduced from pure empirical analysis, that is, they were obtained without any solid theoretical basis but only by careful scientific observation. Using calculus, Kepler’s laws may now be derived theoretically using Isaac Newton’s concept used for deriving his inverse square law of gravity-that is Newton’s inverse square law of universal gravitation which states that the force that acts on any two bodies in the universe is proportional to the product of their masses but inversely proportional to the square of their distance apart.




