Typically, the conic sections, and that includes the ellipse, parabola, and the hyperbola all have their definitions connected to the intersection a plane makes with a cone. However, more technically useful definitions of the conic sections are those provided by plane geometry. The equivalence of the definitions of the conic sections have been proved by Germinal Pierre Dandelin, a Belgian mathematician who discovered the concept now known as the Dandelin spheres in 1822.
The Dandelin spheres which are sometimes called focal spheres can be used to prove some important theorems; at least two. Though the theorems proved by Dandelin have been known for centuries yet Dandelin made it easier to prove them.

The Dandelin Spheres and the closed conic section, that is, the ellipse: The first theorem proved by Dandelin was that of a closed conic section, that is, an ellipse. The theorem states that a closed conic section is the locus of points such that the sum of the distances to fixed foci (that is, two fixed points) is constant.
The second theorem states that for any conic section, the distance from the focus, that is, a fixed point is proportional to the distance from the directrix which is a fixed line and the constant of proportionality is called eccentricity.
As in the case of the first theorem, the second theorem has also been known to the Ancient Greek mathematicians such as Apollonius of Perga but the Dandelin spheres made the proof easier. However, the focus of this article is the first theorem and we shall try to make the proof clearer for easy understanding.
An ellipse as a conic section is the intersection of a cone and a plane such that the angle it made to the vertical is larger than that which the generator of the cone made. In other words, it is the curve resulting from a plane slicing through one of the nappes of the cone and an ellipse has two Dandelin spheres touching the same nappe of the cone (see the diagram below).
However, in plane geometry, an ellipse as a closed conic section is the locus of points such that the sum of the distances to fixed foci (that is, two fixed points) is constant(this is the first theorem proved with the help of Dandelin spheres- see the diagram below).
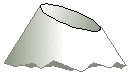
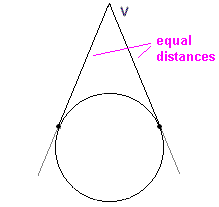
When you first take a glance, it may appear that these definitions do not apply to the same mathematical object but to prove that they are, Dandelin carried out an ingenious construction shown below. If you recall some basic facts from plane geometry, you will be able to see how Dandelin sphere’s construction works. Just consider a circle and a point outside the circle with label V. If you draw two tangents to the circle at point V, then, you will see that the point of tangency are actually at equal distance from V as shown in the diagram below.
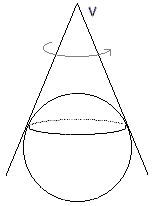
It is straight forward to prove the fact stated above. Look at the symmetry of the situation and consider rotating the figure above about its axis of symmetry, we are able to get an extension to the case of a cone into which a sphere has been inscribed as shown below.
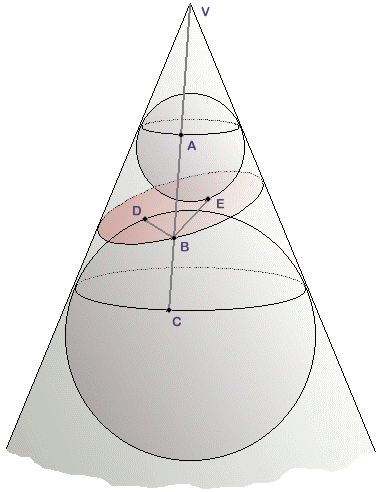
Clearly just as expected, the tangent curve between a sphere and a cone produced a circle. In fact, the circle is such that every point on it is equidistant from the vertex of the cone. Now, if we go back to Dandelin sphere’s construction and we begin with a cone imagining that a plane has passed through the cone thereby producing an ellipse. If we inscribe two spheres in the cone with one sphere above and the other below the ellipse in order for each of them to form a tangent to the cone and to the plane of the ellipse simultaneously. You could even imagine having to fix a spherical balloon in the cone and blow it up so perfectly well until it touches the sides of the cone and the surface of the plane with a perfect fitting.
If you run a straight line through the surface of the cone such that it goes through its vertex, V and take note of its points of intersection with the first circle at point A, the ellipse at point B and the second circle at point C. From the diagram, it is good for you to note that line AC equals line BA and line BC. Also, note that if we take points D and E as the points of tangency between the plane of the ellipse and the two spheres, then BA=BE since each is a tangent that comes from point B to the small sphere. With the same argument, BC=BD (this is, a tangent from B to the large sphere). With simple inference, BA+BC=BD+BE and BA+BC is constant so that BD+BE is also constant.
Therefore, the first theorem is proved which means that a closed conic section, that is, the ellipse, is the locus of points such that the sum of the distances to fixed foci (that is, two fixed points) is constant. Dandelin sphere’s construction can be extended to the parabola and the hyperbola and following similar method as above, they can be proved.




