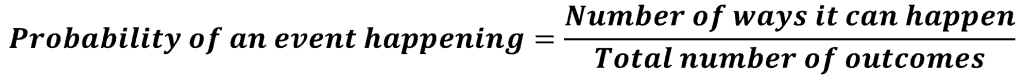We often use the word “probably” in our everyday conversations to emphasize changeability of situations or events. It seems an ordinary word, not the one for scientists. From math’s point of view, probability is quite important, because of managing a wide variety of life processes, but the brain is unable to immediately calculate its value. Here’s a simple at first sight example: “You are stirring the deck of cards. What is the probability that you get the sequence that has already been obtained before by someone else?”. Maybe, you have one chance in 1000 or one of 10,000?
The answer is unexpected, stirring a deck of cards, you create a sequence, that has never previously existed! The reason of such result is connected with function “factorial”, which gives us the number of possible permutations for a given number of objects.
So, what means “the number of possible permutations”?
Suppose, we have only one flower and one pot for it. In how many ways can we situate the given flower in given pot? The answer is obvious 1. Two flowers can be situated in two ways in two pots. But, what happen in the case with 3 flowers – look at the picture below:
In this case, the answer is 6 and it’s impossible to come up with more variants. So, as we’ve mentioned earlier, the number of possible permutations can be reflected with the help of “factorial” and mathematically written as 1!, 2!, 3! for the given examples and n! – generally. If you haven’t met an exclamation mark in mathematics before, learn that it does not mean “Wow! Number!”. It’s just a factorial.
How to calculate the factorial? The simplest thing. Take a number under the factorial sign, and multiply it by all the previous numbers to it, except for zero. For example, 3!=3 × 2 × 1=6. Factorial from 4 is considered as the 4 × 3 × 2 × 1, that is 24. And so on. It seems a quite easy calculation, but only for the first few numbers as five factorial is 120, 6!= 5040 and 7! is already 40320 (for understanding their correct evaluation to check the number of allowable permutations for these numbers ). In fact, even tables or even calculators are constructed for the factorials value. It’s also interesting to mention, that human capabilities are endless.
The Indian woman, Shakuntala Devi, could compute the most complicated arithmetic problems with lightning speed and absolute precision. She was able to calculate the value of 73! in the mind and it took her just 2 minutes for this.
After all the above mentioned, we can turn to the explanation of the prior question, “You are stirring the deck of cards. What is the probability that you get the sequence that has been ever obtained before by someone else?”. As probability of an event happening (in our case, to get the sequence that has been ever obtained before by someone else) will be the ratio below:
Hence, the total number of outcomes will be equal to the number of possible permutations, which is 52!, because there are 52 cards in the deck. According to the table of the factorials value, the number is something like 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277, 824,000,000,000,000. Or 8\cdot 10^{67}, according to the Stirling approximation. Evaluating “the number of ways it may happen”, suppose that 1,000,000 people are stirring the deck of cards every second during 1000 years, then we obtain 1000000\cdot 60\cdot 60\cdot 24\cdot 365000, which is near 32\cdot 10^{15} decks of cards. Substituting these values into our fraction, we get \frac {32\cdot 10^{15}} {8\cdot 10^{67}}=4\cdot 10^{-52}. Thus, the probability you get the sequence that has been ever obtained before by someone else is extremely small, and the probability of getting unique deck of cards will be more than 99,99…999%(number 9 follows the decimal point 52 times). Moreover, our calculation was very rough and the real probability will be even greater. But this is only a 52-card deck. What can we say about the number of parties in the Go (game)?