Recently we’ve discussed what Taylor series is (check our article for more information). In practice, it’s useful to know certain expansions of elementary functions. It’s like a table of derivatives or integrals. If you have it, you’re saving your time in calculations. The case of particular interest is the expansion of function in the vicinity of x=0. Such series is called MacLaurin expansion, and that’s what we’re going to consider for the cases of some common functions. Maclaurin series of elementary functions is widely used and appears frequently in math tasks, so today we’ll obtain it for exponential and logarithmic functions.
But first of all, recall the formula for Maclaurin series:
\sum _{k=0}^{\infty} {\frac {f^{(k)}(0)} {k!}x^k}=f(0)+\frac{f'(0)}{1!}x+\frac{f^{\prime\prime} (0)}{2!}x^2+⋯
Clearly, to get Maclaurin series for the given function we need to find its derivatives at the point x=0 and then just substitute them into the formula above.
Exponential function
Here we have exponential function:
f(x)=e^x
As we consider Maclaurin series, we are going to expand the given function in the vicinity of the point x_0=0. To obtain this expansion we first need to find derivatives of e^x. Luckily, this time we need to do nothing:
(e^x )^{(k)}=e^x
And, evidently:
(e^x )^{(k)}\left.\begin{matrix}\end{matrix}\right| _{x=0}=e^x\left.\begin{matrix}\end{matrix}\right| _{x=0}=1
So we substitute this into general formula and get:
e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+⋯=\sum_{n=0}^{\infty}{\frac{x^n}{n!}}
for x\in R.
Ok, now, let’s see how it looks on the graph.
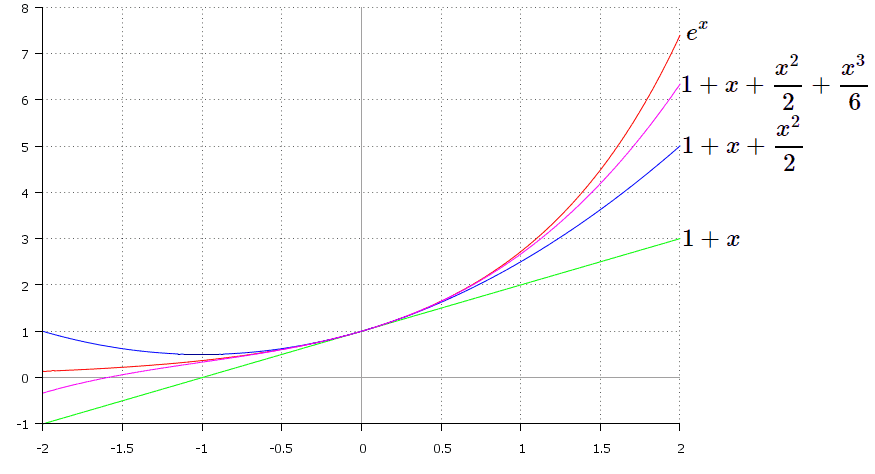
Graph of the initial function e^x is shown in red.
Let’s consider a few approximations of our function in the vicinity of the point x=0. For the first degree approximation we obtain:
f_{approx1}(x) =1+x
It’s just a straight line and goes in green on the graph. For the second degree approximation we get:
f_{approx2}=1+x+\frac{x^2}{2}
Graph of this function is a parabola, marked blue. And for the third degree approximation:
f_{approx3}=1+x+\frac{x^2}{2}+\frac{x^3}{6}
Graph of the last function is a cubic parabola, shown in pink.
As we can see, higher order approximations go closer to the graph of the initial function in the vicinity of $x=0$. If we take infinite number of terms, we’ll obtain exactly the graph of exponential. Keep in mind that unless an infinite sum is in question, Taylor series is only an approximation which resembles the given function to certain derivative and no further.
Q: How many degrees does Taylor claim to have?
A: It depends on the function.
Logarithmic function
We want to construct Taylor expansion of the following function:
f(x)=\ln {(1+x)}
Why we’re considering logarithm of the argument x+1? That’s because we’re expanding it in the vicinity of the point x=0. If we consider \ln{x} instead, we’ll obtain \ln{0} and it doesn’t exist. First of all we need to find derivatives of our function:
(\ln{(1+x)})’=\frac{1}{1+x}
(\ln{(1+x)})^{\prime\prime}=\left ({\frac{1}{1+x}}\right )^{\prime}=-\frac{1}{(1+x)^2} =-\frac{1!}{(1+x)^2}
(\ln{(1+x)})^{\prime\prime\prime}=\left (-\frac{1}{(1+x)^2 }\right )^{\prime}=\frac{2}{(1+x)^3}=\frac{2!}{(1+x)^3}
(\ln{(1+x)})^{(4)}=\left (\frac{2}{(1+x)^3}\right )^{\prime}=-\frac{2\cdot 3}{(1+x)^4} =-\frac{6}{(1+x)^4}=-\frac{3!}{(1+x)^4}
(\ln{(1+x)})^{(5)}=\left (-\frac{2\cdot 3}{(1+x)^4}\right )^{\prime}=\frac{2\cdot 3\cdot 4}{(1+x)^5}=\frac{4!}{(1+x)^5}
Now, we can see a pattern. Sign of derivative alternates, and thus, we can write a derivative in the following general form:
(\ln{(1+x)})^{(n)}=(-1)^{n+1} \frac{(n-1)!}{(1+x)^n}
Since we consider Maclaurin series, we calculate derivatives at the point x=0:
(\ln{(1+x)} )^{(n)} \left.\begin{matrix}\end{matrix}\right| _{x=0}=(-1)^{n+1} \frac{(n-1)!}{1^n}=(-1)^{n+1}(n-1)!
The value of our function at the same point is also required:
\ln{(x+1)} \left.\begin{matrix}\end{matrix}\right| _{x=0}=\ln{1}=0
Now, we can substitute all that stuff into general formula:
\ln{(1+x)}=0+\frac{1}{1!} x-\frac{1!}{2!} x^2+\frac{2!}{3!} x^3-…=x-\frac{x^2}{2}+\frac{x^3}{3}-…=\sum_{n=1}^{\infty}{\frac{(-1)^{n+1} x^n}{n}}
Note that this formula holds only for |x|<1. Let’s see how it will look on the graph.
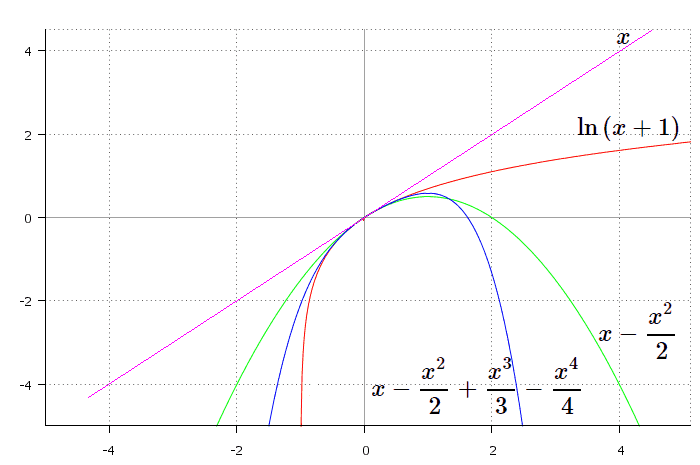
Graph of \ln{(x+1)} is shown in red. For the first degree approximation we get:
f_{approx1}(x) =x
This is a straight line going through the origin, shown in pink. The second degree approximation is a parabola shown in green:
f_{approx2}=x-\frac{x^2}{2}
And for the forth degree approximation we have:
f_{approx4}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}
which goes in blue. As you can see, higher order approximation provides better idea of the initial function behaviour. Of course, this only refers to the vicinity of the point x_0=0.
Often in Taylor series related homework tasks you’ll face functions more complicated than just considered, also you can be asked to expand your function in the vicinity of different point than just zero. Calculations thus are getting complicated and require your attention and time. Luckily, there are lots of online calculators for finding Taylor series, so don’t neglect checking your answers:
Further we’ll show in detail how to obtain two more important expansions, for sine and cosine functions. Stay tuned!






