Have you ever tried to comb a hairy ball? Really, it is a very important and responsible work. It roots back to old 1912. A Holland mathematician Luitzen Brouwer, who worked in a field of topology and set theory, had shown that hairy ball cannot be brushed in such a way to be smooth and without intersections of hairsprings. At least one hairspring should stick up. This result is now called a hairy ball theorem.
It’s easier for mathematicians to consider the hairy ball as the sphere with a so-called vector field on its surface.
In other words, one associates a freely rotating unit vector with each point on the sphere’ surface. So we obtain the sphere with vectors stretching from each point of it (like a hairy ball). The result of such association looks like a hedgehog J (it’s interesting that Russian mathematicians call the Brouwer’s theorem as a theorem about hedgehog brushing). And this hedgehog finds a lot of applications in science and technology.
A direction of motion of air masses can be described by such a vector field. The Earth has a spherical shape, so this vector field is defined on sphere and we can use the hairy ball theorem for analysis. The Earth atmosphere is always in motion: there are winds, ascending and descending flows of air. So, the hairy ball theorem helps to make a conclusion that at least one cyclone should exists. Cyclone is a circular motion of air masses with ascending or descending flow in the origin. And this phenomenon has a purely topological background! Of course, usually meteorologists find more than one cyclone, theorem does not forbid existence of a few unbrushed hairsprings.
Francesco Sellacci from MIT has shown an elegant usage of the hairy ball theorem in 2007. He worked in the field of manufacturing of nanoparticles and tried to make elongated chains of spherical nanoparticles. Nano-sized golden balls were covered by long molecules with sulfur atoms on their ends. Sulfur is strongly bonded with gold. It is a reason why electricians do not like it so much: it reduces conductivity of golden contacts. But in our case sulfur only fixes molecules on nanoparticles. They work as hairsprings. According to the hairy ball theorem there will be places, where molecules cannot fit tightly against the surface. Different nanoparticles will be bonded one to another in these places.
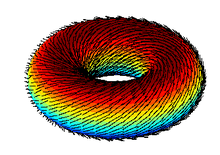
Everything written above is about sphere and similar shapes without holes. But if we take a torus (a doughnut), we can comb it smoothly.
Really, the surface of torus can be cut up and unrolled into rectangle unlike the sphere. So, any homogeneous vector field on its surface will hold the condition of smooth combing.
There is an optimal solution for a sphere/ball: it is a spiral which will end up at the end/bottom with only one hair pointing up 😉