Graphical representation of the x-and y-intercepts is quite simple. The intercepts at the x-axis, called x-intercepts are points where the graph crosses the x-axis while the intercepts at the y-axis, called the y-intercepts are points where the graph crosses the y-axis. However, the main challenge of the intercepts comes when we attempt to provide algebraic expressions and equations to the x-and y- intercepts.
In order to understand the algebraic part of intercepts, you would need to recall the elementary idea of the number line and the Cartesian plane. Draw a perpendicular number line, that is the y-axis, through the zero point on the horizontal (x-axis) line and you will see that the y-axis is the line ‘’x=0’’ and the x-axis is the line ‘’y=0’’. Therefore, algebraically, we conclude as follows:
1. Any given x-intercept is a point on the Cartesian graph where y=0, and
2. Any given y-intercept is a point on the Cartesian graph where x=0.
In terms of equations, we can write the above statements to mean that an x-intercept is a point in the equation where the value of y=0 while a y-intercept is a point in the equation where the value of y=0. In addition, you need to understand that the following three algebraic equations mean the same thing:
1. If y = x3+5x2-x- 1, find the x-intercepts.
2. If x3 + 5x2 – x – 1=0, then, solve the equation completely.
3. If f(x) = x3 + 5x2 – x – 3, find the roots or zeroes of the function. If you understand the equivalence of these three algebraic equations, you will be able to understand and solve many exercises.
Graphical Exercises:
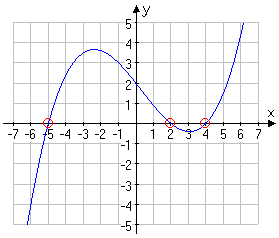
If the graphical representation of the algebraic equations like the following graph is given and you are asked to find the solutions, then, you need to know that you are asked to find the x- intercepts though you were never given the equation.
The graph: