Medieval mathematician and businessman Fibonacci (Leonardo Pisano) posed the following problem in his treatise Liber Abaci (pub. 1202):
How many pairs of rabbits will be produced in a year, beginning with a single pair, if in every month each pair bears a new pair which becomes productive from the second month on?
This problem can be illustrated in such way:
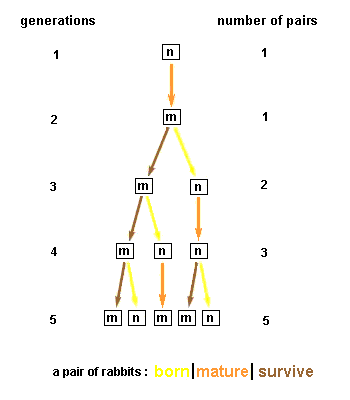
Suppose a pair of rabbits, one male and one female, start a family. Rabbits mature at the age of one month (labeled “m”) and a female produces a new pair of rabbits (labeled “n”) at the end of its second month. Suppose that the rabbits survive forever and that a female always produces one new pair (one male, one female) every month, giving the original pair and a new one.
It is easy to see that 1 pair will be produced the first month, and 1 pair also in the second month (since the new pair produced in the first month is not yet mature), and in the third month 2 pairs will be produced, one by the original pair and one by the pair which was produced in the first month. In the fourth month 3 pairs will be produced, and in the fifth month 5 pairs. After this, things expand rapidly, and we get the following sequence of numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
This is an example of a recursive sequence, obeying the simple rule that to calculate the next term one simply sums the preceding two:
F(1) = 1
F(2) = 1
F(n) = F(n – 1) + F(n – 2)
Thus 1 and 1 are 2, 1 and 2 are 3, 2 and 3 are 5, and so on.
The Fibonacci sequence can be obtained as a sequence of ratios of consecutive Fibonacci numbers:
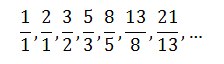
This sequence converges, that is, there is a single real number which the terms of this sequence approach more and more closely, eventually arbitrarily closely. The value of it equals to
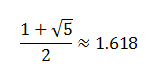
This number was known to the ancient Greeks and was called by them the Golden Mean. It is usually denoted by the Greek letter φ (phi), and sometimes by μ (mu). They believed that the proportion φ:1 was the most pleasing, indeed the aesthetically perfect proportion, and all of their artwork, sculpture, and especially architecture made use of this proportion. A rectangle whose sides had this proportion was called the Golden Rectangle.
The Fibonacci series is defined recursively. That is, in order to find each term of the series using the definition, you have to find all the terms that precede it. This makes finding the n-th term very difficult for large values of n, as you must find every term that comes before.
However, there could be a way to find Fibonacci numbers without using the definition. If this were possible, one would be able to find the nth term of the series simply by plugging n into a mathematical formula. You can use the Binet’s formula, Binomial approximation, and the Successor Formula which are derived by famous mathematicians to achieve these purposes.
The Fibonacci numbers are well-used in many branches of Science and can be found in the Nature:
- The Fibonacci numbers are important in the computational run-time analysis of Euclid’s algorithm to determine the greatest common divisor of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.
- Yuri Matiyasevich was able to show that the Fibonacci numbers can be defined by a Diophantine equation, which led to his original solution of Hilbert’s tenth problem.
- The Fibonacci numbers occur in the sums of “shallow” diagonals in Pascal’s triangle and Lozanić’s triangle (see Binomial coefficient). They occur more obviously in Hosoya’s triangle.
- Every positive integer can be written in a unique way as the sum of one or more distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers.
- The Fibonacci numbers and principle is also used in the financial markets. It is used in trading algorithms, applications and strategies.
- Fibonacci numbers are used by some pseudorandom number generators.
- In music, Fibonacci numbers are sometimes used to determine tunings, and, as in visual art, to determine the length or size of content or formal elements. It is commonly thought that the third movement of Béla Bartók’s Music for Strings, Percussion, and Celesta was structured using Fibonacci numbers.
- Fibonacci sequences appear in biological settings, in two consecutive Fibonacci numbers, such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple, the flowering of artichoke, an uncurling fern and the arrangement of a pine cone.
- In addition, numerous poorly substantiated claims of Fibonacci numbers or golden sections in nature are found in popular sources, e.g. the spirals of shells, and the curve of waves. The Fibonacci numbers are also found in the family tree of honeybees.
sources:
https://library.thinkquest.org
https://en.wikipedia.org
https://www.mathacademy.com/

