Quite often students have some problems with understanding the concept of the vector space basis, the linear dependence and linear independence of the vectors. In this article, we’ll try to explain these terms through simple things and examples. If you still don’t know what the vector is or don’t know how to do simple operations with vectors we offer you to watch our introductory video tutorial and then continue reading this article.
In the video, we really explain what a vector is. But what do the linearly dependent vectors mean? Let’s distract a bit and look at the plane of your computer desk (or another table, cupboard, floor, ceiling, etc.). Your task is the following: select a basis of the plane. As you know, the tabletop has the length and the width, but we don’t count the thickness of the tabletops. So we need two basis vectors to determine the table plane (one vector is clearly not enough while three vectors are too much).
Explanation is quite simple; you should only place your left index finger on the edge of the table so that it could look at the monitor. This is a vector \overline{e_1}. Now, place the little finger of the right hand on the table in the same way (it should be directed at the screen). This is a vector \overline{e_2}.
What can be said about vectors \overline{e_1}, \overline{e_2} ? These vectors can be linearly expressed in terms of each other \overline{e_1}=\alpha \overline{e_2}. (“linearly” means there are no squares, cubes, and other powers, logarithms, sine, etc. in mathematical equations or expressions).
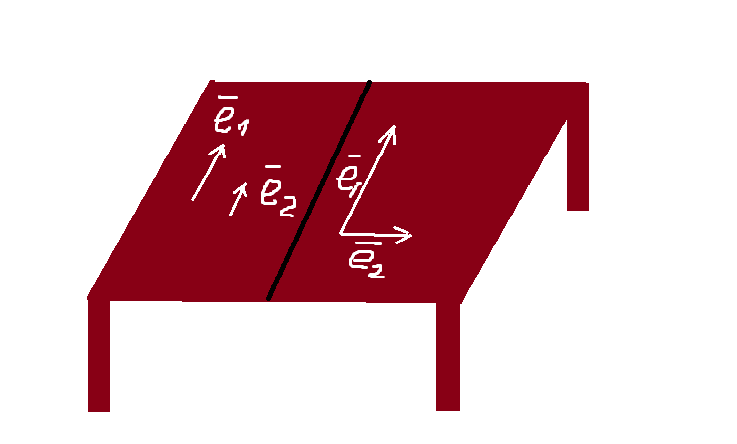
Will your fingers set the basis of the computer desktop plane? Obviously, no. Collinear vectors travel back and forth in one direction, while the plane has a length and width. Cross your fingers on the table to make any angle (except 0 and 180 degrees). Consequently, the basis (\overline{e_1}, \overline{e_2}) is obtained, and in this case, we get linearly independent vectors.
Here you should remember: the vectors can be either linearly dependent or linearly independent.
Two vectors \overline{v}=(v_1,v_2), \overline{w}=(w_1,w_2) are linear dependent if and only if their corresponding coordinates are proportional
<br /> \begin{cases}<br /> \overline{v_1}=\alpha \overline{w_1}\\<br /> \overline{v_2}=\alpha \overline{w_2}\\<br /> \end{cases}
If this condition is not met, then the vectors will be linearly independent. Now let’s solve one of the tasks, which you can often find in your homework or exam: determine whether the vectors \overline{a}=(3,7) and \overline{b}=(-6,14) form a basis.
Two vectors of the plane form a basis, if they are linearly independent. We’re going to determine whether there is proportionality factor \alpha for vectors \overline{a}=(3,7) and \overline{b}=(-6,14), which makes equalities truthful
<br /> \begin{cases}<br /> \overline{a_1}=\alpha \overline{b_1}\\<br /> \overline{a_2}=\alpha \overline{b_2}\\<br /> \end{cases}\implies\begin{cases}<br /> 3=\alpha \cdot (-6)\Rightarrow \alpha=-\frac{1}{2}\\<br /> 7=\alpha \cdot 14\Rightarrow \alpha=\frac{1}{2}\\<br /> \end{cases}
This system has no solutions, which means that the respective vectors’ coordinates are not proportional.
Hence, the conclusion is: the vectors are linearly independent and form a basis.
However, there is an elegant algebraic method to check vectors for collinearity: the determinant, which is formed from the coordinates of the collinear vectors, equals zero. Let’s see how this works: determine whether the vectors below form a basis \overline{a}(4,-2,2),\overline{b}(-3,3,-4),\overline{c}(2,-4,3)
Let us calculate the determinant, which is formed from the vectors’ coordinates, placed in columns. Besides, for more information on how to find the determinant – see our video Calculating Determinants.
\begin{vmatrix}4 & -3 & 2 \\ -2 & 3 & -4 \\ 2 & -4 & 3\end{vmatrix} =4\begin{vmatrix}3 & -4 \\ -4 & 3 \end{vmatrix}+3\begin{vmatrix}-2 & -4 \\ 2 & 3 \end{vmatrix}+2\begin{vmatrix}-2 & 3 \\ 2 & -4 \end{vmatrix}=4(9-16)+3(-6+8)+\\ +2(8-6)=-28+6+4=-18\neq 0
It means the vectors are linearly independent and form a basis.
We hope this explanation will be useful for you. If you have any other problems with math, you can put your questions on our homework answers page if they don’t require much time to be answered and we’ll be happy to help you for free. But in case you have really difficult problems, please address experts on our website to get a proficient homework help for a reasonable price timely and with 98% guarantee of the successful grade.