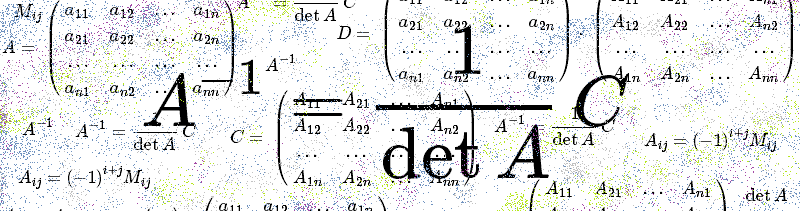Inverse matrices are widely applied. For example, suppose you’re asked to perform matrix division in your linear algebra homework. As we said in one of previos articles about basic matrix operations, matrix division is in fact multiplication by an inverse matrix. If you are going to solve a system of equations in matrix representation you’ll also need to find inverse matrix. So let’s talk about inverse matrices and how to find them.
First of all, what is inverse matrix? Matrix B is called inverse to the square matrix A if B satisfies the following equality:
AB=BA=E
where E is a unit matrix. So an inverse matrix for given is such matrix which multiplied by initial one gives unit matrix. It follows from the definition that inverse matrix exists only for square matrix and both are of the same size. Matrix inverse to matrix A is denoted as A-1.
Ok, but how do we find an inverse for given matrix? That requires some calculations, let’s see.
Consider square matrix of n-th order:
A=\begin{pmatrix}a_{11} & a_{12} & … & a_{1n} \\a_{21} & a_{22} & … & a_{2n} \\… &… & …& …\\a_{n1}& a_{n2}& … & a_{nn}\end{pmatrix}
Also consider another matrix which looks like following:
C=\begin{pmatrix}A_{11} & A_{21} & … & A_{n1} \\A_{12} & A_{22} & … & A_{n2} \\… &… & …& …\\A_{1n}& A_{2n}& … & A_{nn}\end{pmatrix}
The latter is so called adjugate matrix to matrix A. Here Aik is an algebraic cofactor(also reffered to as signed minor) of entry aik of matrix A. Recall the formula relating cofactors and minors of a matrix:
A_{ij}=(-1)^{i+j}M_{ij}
Mij is called minor of matrix A and is a determinant of matrix obtained by removing row “i” and column “j” from initial matrix A.
Note that algebraic cofactors of elements in i-th row of matrix A are situated in i-th column of matrix C.
The following theorem takes place: if A is a square matrix of n-th order, C is the adjugate matrix for matrix A, then
AC=CA=E \det A
where E is a unit matrix of n-th order.
Let’s denote matrix product AC=D, i.e.
D=\begin{pmatrix}a_{11} & a_{12} & … & a_{1n} \\a_{21} & a_{22} & … & a_{2n} \\… &… & …& …\\a_{n1}& a_{n2}& … & a_{nn}\end{pmatrix}\cdot\begin{pmatrix}A_{11} & A_{21} & … & A_{n1} \\A_{12} & A_{22} & … & A_{n2} \\… &… & …& …\\A_{1n}& A_{2n}& … & A_{nn}\end{pmatrix}
Due to definition of matrix product, element dik of matrix D equals to the sum of products of elements in the i-th row of matrix A by corresponding elements of k-th column in matrix C, where C is the adjugate for matrix A. For elements dii (i=1,2,…,n), which lye on main diagonal, this sum equals to determinant of matrix A (due to the theorem of determinant expansion by the elements of any row), for the rest elements dik (i is nit equal to k) this sum equals zero. Therefore:
D=AC=\begin{pmatrix}\det A & 0& … & 0\\0 & \det A & … & 0 \\0 &0& …& 0\\0& …&0 & \det A\end{pmatrix}
Similarly it’s proved that CA=E \det A
Square matrix is called invertible (some authors use nonsingular or nondegenerate) if its determinant is not zero. If determinant of matrix is zero then it’s called degenerate or singular.
The following theorem takes place. For nonsingular matrix A there exists unique inverse matrix A-1 defined by the following formula:
A^{-1}=\frac{1}{\det A}C
where C – adjugant matrix for matrix A.
Since A is nonsingular then its determinant is non-zero:
\det A\neq 0
We said before that AC=CA=E \det A
whence we obtain
A(\frac{1}{\det A}C)=(\frac{1}{\det A}C)A=E
It means that equality AB=BA=E from the definition of inverse matrix holds therefore matrix A^{-1}=\frac{1}{\det A}C is really an inverse matrix for matrix A. Inverse matrix for the given matrix A is unique.
Now let’s consider an example. Let’s find an inverse for the following matrix:
A=\begin{pmatrix}2 & 0 &-1\\-3 & 1 & 1 \\2& -1& 0\end{pmatrix}
Here’s video version of this example, take a look!
First of all, we need to calculate the determinant of the give matrix:
\begin{aligned} \det A&=\begin{vmatrix}2 & 0 &-1\\-3 & 1 & 1 \\2& -1& 0\end{vmatrix}=2\cdot 1\cdot 0+0\cdot 1\cdot 2+(-3\cdot (-1)\cdot (-1))\\&-(-1\cdot 1\cdot 2+(-1\cdot 1\cdot 2)+0\cdot 2\cdot 0)=-3+2+2=1\end{aligned}
After that we need algebraic cofactors (mind the sign!):
A_{11}=(-1)^{(1+1)} \cdot \begin{vmatrix}1 &1 \\-1& 0\end{vmatrix}=1
A_{12}=(-1)^{(1+2)} \cdot \begin{vmatrix}-3 &1 \\2& 0\end{vmatrix}=-1 \cdot (-2)=2
A_{13}=(-1)^{(1+3)} \cdot \begin{vmatrix}-3 &1 \\2& -1\end{vmatrix}=3-2=1
A_{21}=(-1)^{(2+1)} \cdot \begin{vmatrix}0 &-1 \\-1& 0\end{vmatrix}=-1 \cdot (-1)=1
A_{22}=(-1)^{(2+2)} \cdot \begin{vmatrix}2 &-1 \\2& 0\end{vmatrix}=2
A_{23}=(-1)^{(2+3)} \cdot \begin{vmatrix}2 &0 \\2& -1\end{vmatrix}=-1 \cdot (-2)=2
A_{31}=(-1)^{(3+1)} \cdot \begin{vmatrix}0 &-1 \\1&1\end{vmatrix}=1
A_{32}=(-1)^{(3+2)} \cdot \begin{vmatrix}2 &-1 \\-3&1\end{vmatrix}=-1 \cdot (2-3)=1
A_{33}=(-1)^{(3+3)} \cdot \begin{vmatrix}2 &0 \\-3&1\end{vmatrix}=2
Using the formula for inverse matrix we’ve discussed above and substituting values we’ve just calculated we obtain inverse matrix for matrix A:
A^{-1}=\frac{1}{1} \cdot \begin{pmatrix}1 & 1 & 1 \\2 & 2&1 \\1& 2&2\end{pmatrix}=\begin{pmatrix}1 & 1 & 1 \\2 & 2&1 \\1& 2&2\end{pmatrix}
We can check if our result is correct by multiplying A and A-1. If we’ve done our calculations correctly, the result should be unit matrix E. Let’s see:
AA^{-1}=\begin{pmatrix}2 &0 & -1 \\-3 & 1 &1\\2& -1&0\end{pmatrix} \cdot \begin{pmatrix}1 & 1 & 1 \\2 & 2&1 \\1& 2&2\end{pmatrix}=\begin{pmatrix}1 &0 &0 \\0& 1 &0\\0& 0&1\end{pmatrix}
Don’t omit checking the answers when doing math homework, thus you can be sure you’ve done the task correct. It’s especially important in matrix problems because it’s easy to slip up when working with such large amounts of calculation. Along the line, for cheking homework tasks you can also use online math calculators which are of great help; keep in mind that you can’t fully rely on them because on your test or exam you won’t be allowed to use them.
Mentioned way of finding inverse matrix is not the only one. There are various methods, among them Gaussian elimination method, we’ll show how to apply it in one of the next sections.
