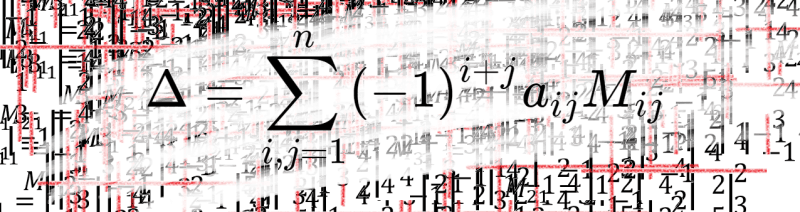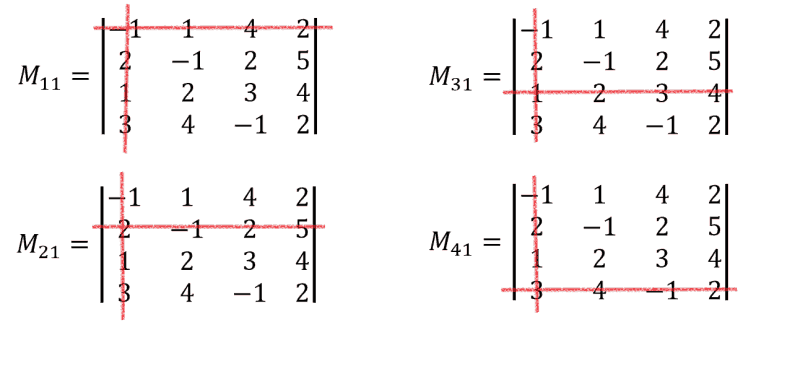We’re continuing to prepare math tutorials. Hopefully, it will be helpful for you and you won’t be in need asking our experts something like “Do my math homework for me, please! I’m stuck..” This is the second part of our tutorial explaining how to calculate determinants. We’re asked to calculate the determinant of the following 4×4 matrix:
A=\begin{pmatrix}-1 & {1} & 4 & 2 \\2 & -1 & 2 & 5 \\1 &2 & 3& 4\\3& 4& -1 & 2\end{pmatrix}
Recall that only square matrices have a determinant, for non-square ones it’s not defined. Matrix A is a square 4×4 matrix so it has determinant. Here we have no zero entries, so, actually, it doesn’t matter what row or column to pick to perform so called Laplace expansion. Let it be the first column. It means that we set j=1 in general formula for calculating determinants which works for determinants of any size:
\Delta =\sum_{i,j=1}^{n}(-1)^{i+j}a_{ij}M_{ij}
Another index i is changing from 1 to 4 (n=4 because A is 4×4 matrix). Substituting the values into general formula we obtain:
\begin{aligned} \Delta &=\sum_{i,j=1}^{4}(-1)^{i+j}a_{i1}M_{i1}\\&=(-1)^{1+1}a_{11}M_{11}+(-1)^{2+1}a_{21}M_{21}+(-1)^{3+1}a_{31}M_{31}+(-1)^{4+1}a_{41}M_{41}\\&=a_{11}M_{11}-a_{21}M_{21}+a_{31}M_{31}-a_{41}M_{41}=-1\cdot M_{11}-2 \cdot M_{21}+1\cdot M_{31}-3 \cdot M_{41} \end{aligned}
Here’s video version of this tutorial:
To find the value of \Delta we need to calculate minors M_{11}, M_{21}, M_{31}, M_{41}. These are the determinants of order 3×3:
Let’s calculate them in the same way, but choosing the first row. It means, we set i=1, while j is changing from 1 to 3. Note that this time upper limit equals 3 instead of 4 for the initial determinant, because these are determinants of the size 3×3. In general we could pick any row or column we want:
\begin{aligned} M_{11}&=\begin{vmatrix}-1&2 &5 \\2& 3 &4 \\4&-1 &2\end{vmatrix}=-1 \cdot\begin{vmatrix}3&4 \\-1&2 \end{vmatrix}-2\cdot\begin{vmatrix}2&4 \\4&2 \end{vmatrix}+5\begin{vmatrix}2&3 \\4&-1\end{vmatrix}\\&=-1\cdot (6+4)-2\cdot (4-16)+5\cdot(-2-12)=-10+24-70=-56\end{aligned}
Similarly we calculate the rest three minors:
\begin{aligned} M_{21}&=\begin{vmatrix}1&4&2 \\2& 3 &4 \\4&-1 &2\end{vmatrix}=1 \cdot\begin{vmatrix}3&4 \\-1&2 \end{vmatrix}-4\cdot\begin{vmatrix}2&4 \\4&2 \end{vmatrix}+2\begin{vmatrix}2&3 \\4&-1\end{vmatrix}\\&=1\cdot (6+4)-4\cdot (4-16)+2\cdot (-2-12)=10+48-28=30\end{aligned}
\begin{aligned} M_{31}&=\begin{vmatrix}1&4&2 \\-1& 2 &5 \\4&-1 &2\end{vmatrix}=1 \cdot\begin{vmatrix}2&5 \\-1&2 \end{vmatrix}-4\cdot\begin{vmatrix}-1&5 \\4&2 \end{vmatrix}+2\begin{vmatrix}-1&2 \\4&-1\end{vmatrix}\\&=1\cdot (4+5)-4\cdot (-2-20)+2\cdot (1-8)=9+88-14=83\end{aligned}
M_{41}=\begin{vmatrix}1&4&2 \\-1& 2 &5 \\2&3 &4\end{vmatrix}=1\cdot (8-15)-4\cdot (-4-10)+2\cdot (-3-4)=-7+56-14=35
Finally we have all the necessary data for finding the required determinant. Let’s substitute the values into the expression for \det A:
\begin{aligned} \Delta& =-1\cdot M_{11}-2 \cdot M_{21}+1\cdot M_{31}-3 \cdot M_{41}\\&=-1\cdot (-56)-2\cdot 30+1\cdot 83-3\cdot 35=56-60+83-105=-26\end{aligned}
Thus, the answer is:
\det A =-26
Summing up. If you’re asked to calculate the determinant of some matrix, first of all make sure you’re dealing with a square one, i.e. the number of rows and the number of columns are the same. If it’s so, then you can proceed and apply general formula for calculating determinants which goes as follows:
\Delta =\sum_{i,j=1}^{n}(-1)^{i+j}a_{ij}M_{ij}
Here $n$ is the size of your square matrix. Next you pick some row or column and perform expansion, getting thus a bunch of smaller determinants to calculate. For convenience choose the row or column with smallest values or better with zeros if possible. Such approach will save you time and allow to do you math homework faster.
More math in our next sections!