Answer to Question #113174 in Microeconomics for ardil

Question

. For the following LP problem, graph the region of feasible solution and solve by the corner-point method.
Maximize z = 4x1 + 8x2
Subject to 4x1 + 6x2 ≤ 48
x1 + x2 ≥ 15
x1 , x2 ≥ 0


For the following LP problem, graph the region of feasible solution and solve by the corner-point method.

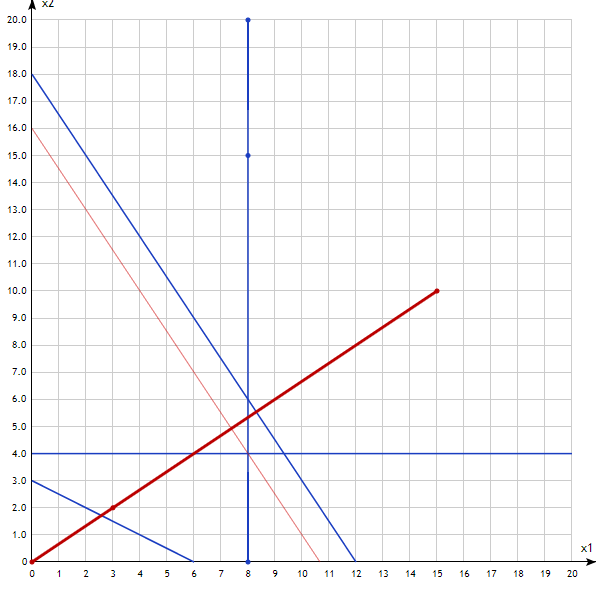
Minimize z = 3x1 + 2x2
Subject to x1 + 2x2 ≥ 6
9x1 + 6x2 ≤ 108
x1 ≥ 8
x2 ≥ 4
x1 , x2 ≥ 0

Answer 1

$$z=4x_1+8x_2 \to max$$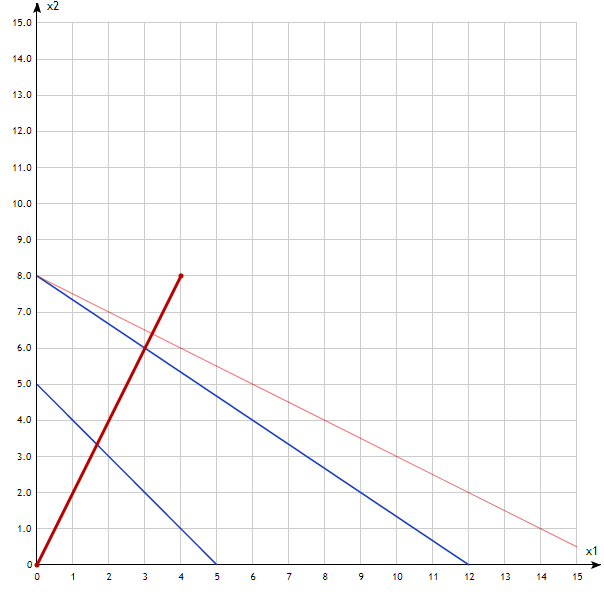

The red thick line shows the gradient of the objective function, the red thin line shows the level line so that the indicated region remains in the region in which the values ​​of the objective function are accepted that are smaller than this.

We see that this function reaches its maximum value at a point with coordinates (0; 8)

$$z_{max}=4\times 0+8 \times 8=64$$

$$z=3x_1+2x_2 \to min$$

Arguing in a similar way, we see that this function reaches its minimum value at a point with coordinates (8; 4)

$$z_{min}=3\times8+2\times4=24+8=32$$