Recently, the term “catastrophe” started to appear not only in the newspaper articles and TV news but also in… mathematics! The first signs of the catastrophe theory emerged in the early 70s and provoked a revolution in mathematics. This achievement is only comparable to the invention of integral and differential calculus. While Newton’s theory allows investigating smooth, continuous processes, catastrophe theory provides a universal “recipe” for the study of abrupt transitions, ruptures and sudden qualitative changes.
The mathematical sources of catastrophe theory are the singularity theory of smooth maps and bifurcation theory of dynamical systems. In fact, the singularity theory is only a generalization of the research functions on the maxima and minima, which can be found by students in the calculus course. Bifurcation theory considers the qualitative metamorphosis of the different objects (systems) when changing the parameters which they depend on, in other words, what the jumping parameters can lead to a catastrophe or the preservation of balance.
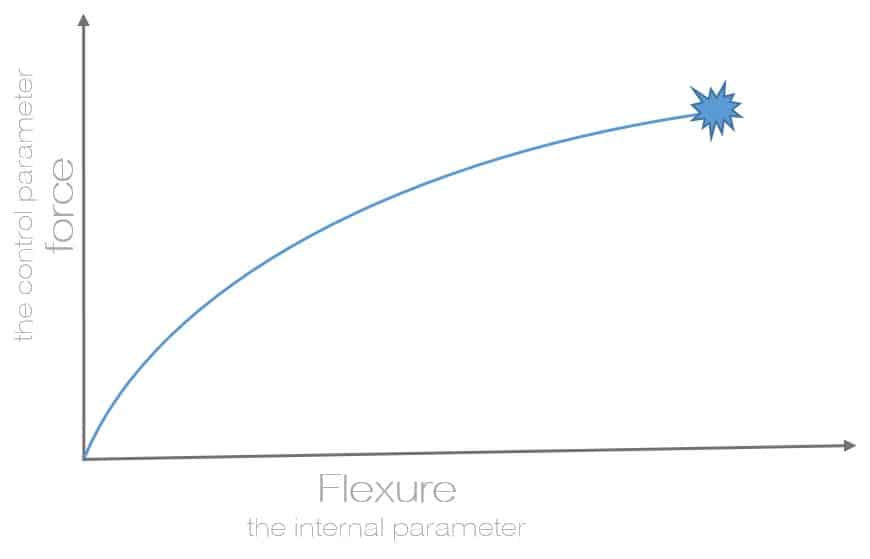
Catastrophe is the abrupt change in the form of a sudden system response to a smooth change in the external conditions. Imagine that you bend the wooden ruler. It is bending for some time, and then it suddenly breaks down. This example allows us to understand the essence of the considered. While the applied force (control parameter) is perpendicular to the plane of the ruler, its bend (internal parameter) changes slowly at first, and then – abruptly. This relationship is illustrated with the help of a simple graph.
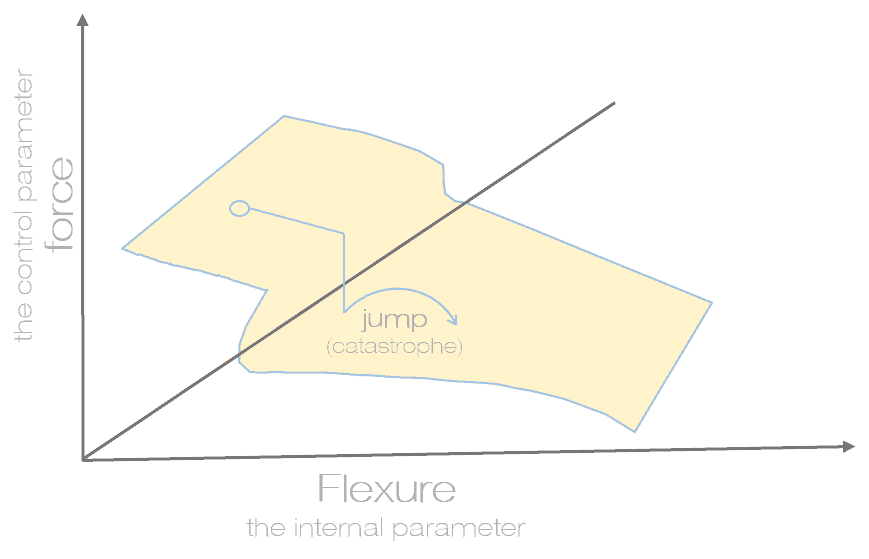
But if the model is a bit complicated and a variable angle between the ruler and the direction of the force is selected as a second control parameter, the dependence immediately ceases to be simple. It can be only expressed in a three-dimensional surface of the complicated shape.
Thus, depending on the initial conditions, the catastrophe with a ruler, which is dependent on two control parameters, can be represented as a border crease on the surface or as a bend. In mathematics, different types of catastrophe are classified. The simplest of them is “the crease”, next goes “the assembly”, which is also followed by more complex catastrophes. The total number consists of 20 types, and each of them has its own characteristics.
According to the catastrophe theory, we propose the following model of system functioning (economic, environmental, social, technical). Any system passes through its stages of development: the stage of growth (formation), stage of the existence and stability, stage of the crisis (fading, dying, reconstruction, modernization). The crisis is completed by a destruction of the system or its transferring to a new higher condition.
The described theory is widely applied to a variety of scientific fields, such as embryology, cardiology, psychology, linguistics, economics, sociology and geology, not to mention such “natural” disciplines like optics, theory of stability of elastic structures and ships at excitement or, for example, the theory of elementary particles. Among the publications on the theory of catastrophes, the most extraordinary are on mental disorders and prisoners’ rebellions, the behavior of stockbrokers, the impact of alcohol on drivers and even censorship on erotic literature.