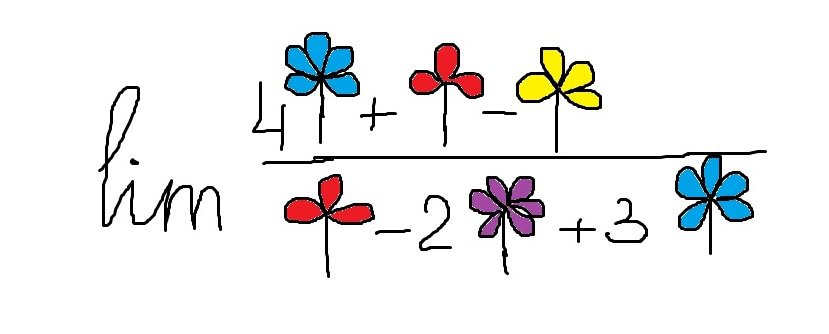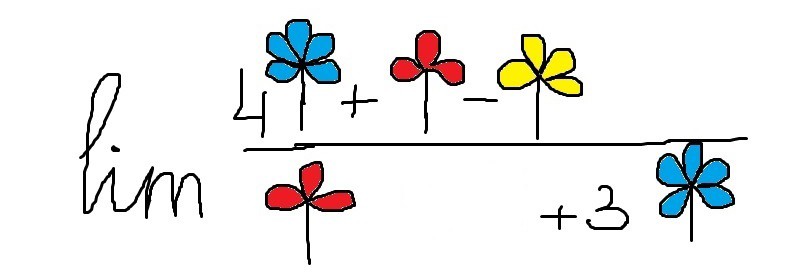Solving math problem, especially in the high school, requires using a wide variety of theorems, lemmas, their corollaries. However, quite often students face misunderstandings during the math lectures, which bring troubles with solving these practical exercises. But how to remember all the math stuff? Here we’ll offer you one of the methods. This interesting and useful technique deals with the association of the difficult problems with the simple things.
Let’s consider limits where the function is represented as a fraction of polynomials and where x tends to infinity.
\lim_{x \to \infty} \frac{4x^5+x^3-x^4}{x^3-2x^6+3x^5}
One of the explanations of evaluating such kind of the limits you can watch from our video
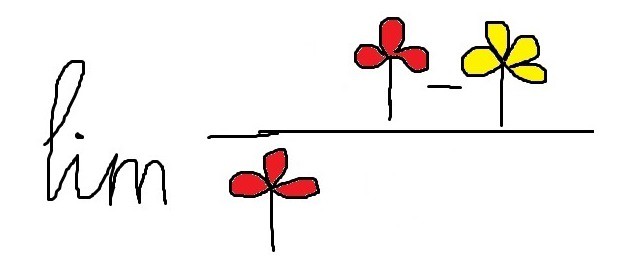
In this video, Max gives a very simple explanation, but if you haven’t understood it yet, we offer you “The Flower Math”. OK, sounds strange, but let’s try and you’ll like it. Imagine we have flowers instead of variable x; let the powers of x be the number of flower petals. The given limit can be represented in the following way (sorry, we haven’t found a professional artist among our experts)
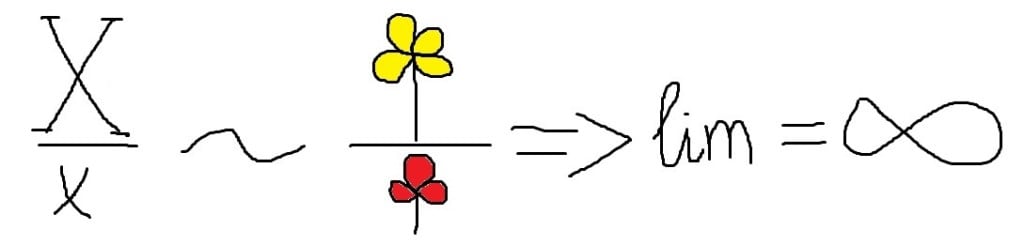
Now, we should find the coolest flower – the one that has the biggest number of petals. It’s obvious that the coolest flower here is the purple one below the line, because it has 6 petals (this is similar to one of the cases in video, when x with highest power was below the line). So, what do we have?
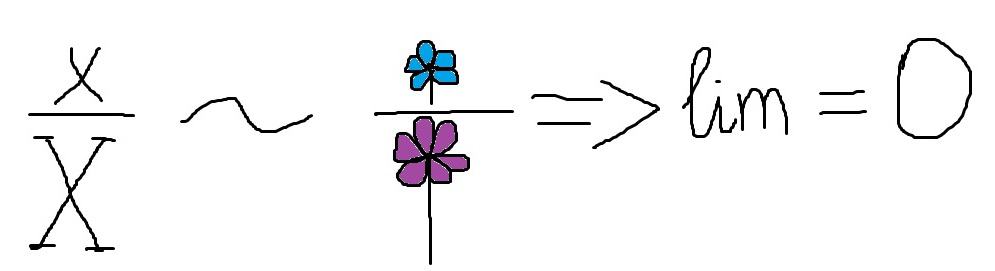
If we pull out purple flower, we’ll obtain two coolest flowers, which are blue
Such lim is similar to the case when x had the same highest powers being over and below the line.
But if we pull out these blue flowers, we will have the following
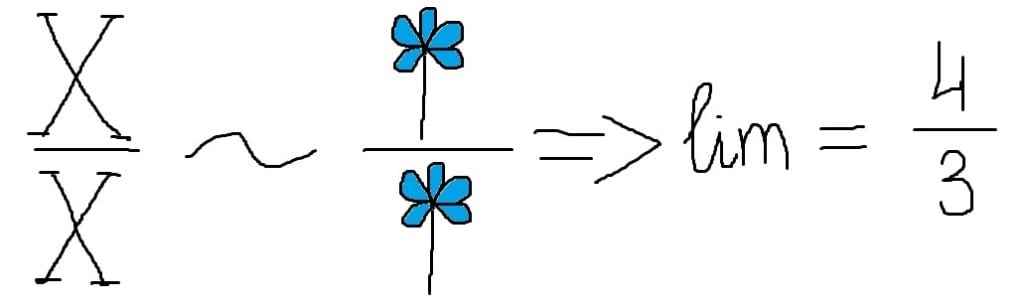
And well, it’s obvious that now yellow flower becomes the coolest flower similarly to x with the highest power over the line. Being over the line (being the coolest, you know) associates exactly with infinity in the result of limit evaluation.
That’s the whole science behind the flower math of such limits. But pay attention that the described method is quite rough approximation to the limits theory. It gives you the opportunity to better grasp the rules, but it can also have some inaccuracies, so it’s only additional technique for your memorization.
