Every day each of us listens to music, views images on the Internet, turns on a radio station or a TV channel. All these processes have a common feature; it is their implementation involving the use of the same mathematical tool – the Fourier transform. It’s not an exaggeration to say that this is one of the most widely used mathematical discoveries, which is widely known in optics and quantum physics, radio astronomy, X-ray crystallography, voice recognition and PET (positron emission tomography) or MRI (magnetic resonance imaging), etc.
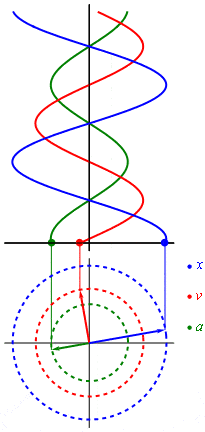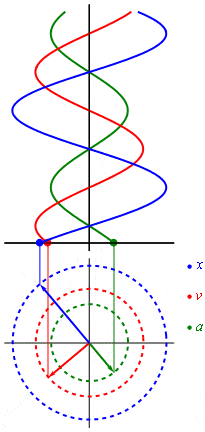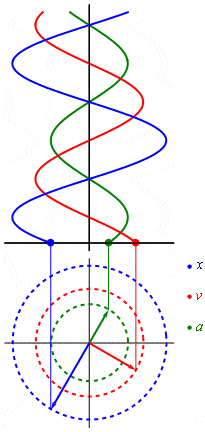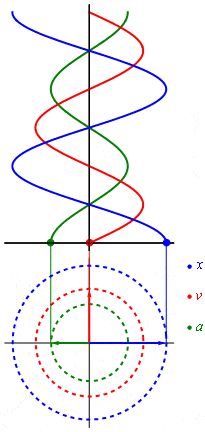
So what did Fourier discover and what is it useful for? Imagine you are playing the piano. When you press the button, the hammer strikes the string, which vibrates with a certain frequency (440 times per second). While the string is vibrating, air molecules jump up and down around it, creating a wave of the swaying air molecules, which we call a sound. If you could observe how the air makes this periodic dance, you would see a continuous infinitely repeated wavelike curve, which is called a sinusoid.
If you remember the school math classes, then using a circle to build a sine graph should be familiar to you. Overall, the rotary motion (as well as any harmonic oscillation) can be converted into a sine wave. The best illustration of this process may be found on Wikipedia. The magic begins with the fact that absolutely any signal can be represented as the sum of (often infinite) different sinusoids. In other words, in the form of a Fourier series.
Fourier’s idea included not just a special property of musical chords, but a general property of any recurring wave – square, round, twisting, triangular, whatever. Fourier Transform is similar to the mathematical prism, where you provide the wave to the input and obtain the components of this wave (or sine wave) in the output.
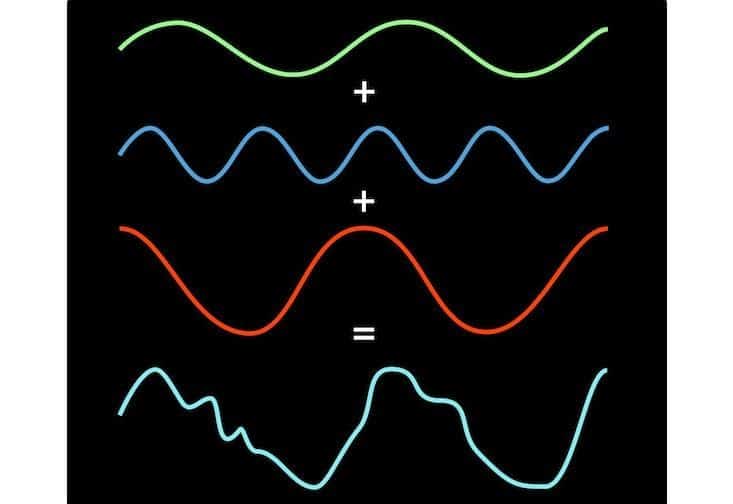
Here are a few ways of visualizing Fourier’s ideas:
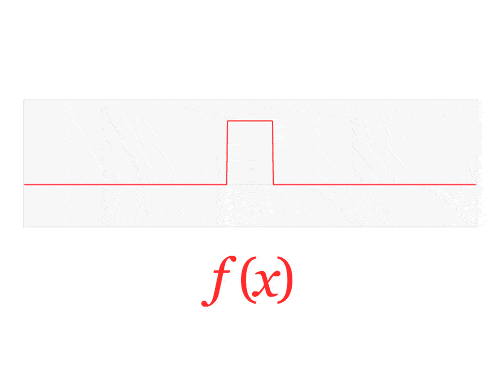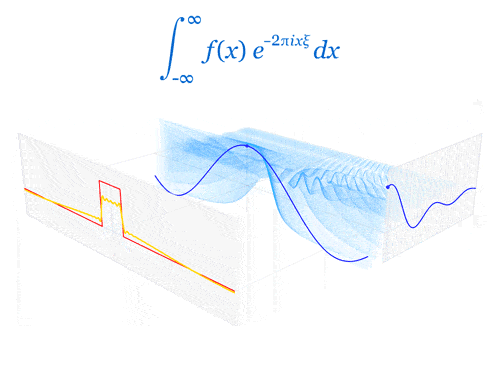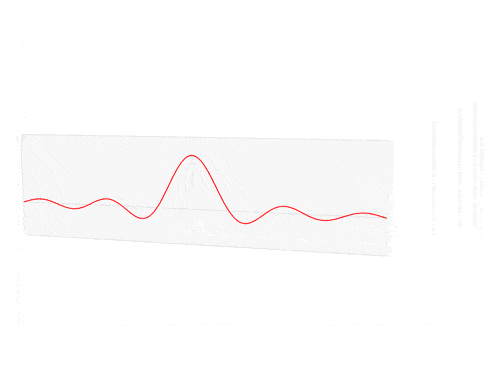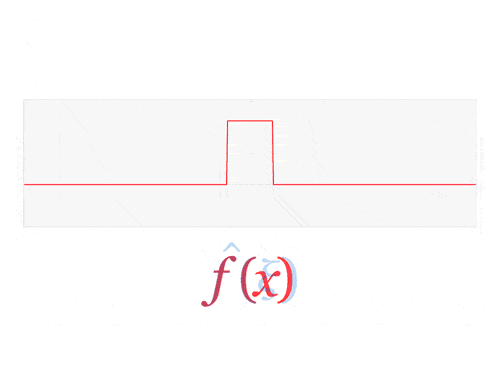
Fourier transform of the rectangular function and cardinal sine functions.
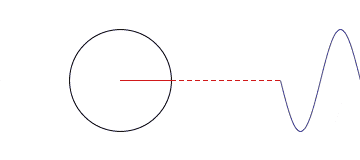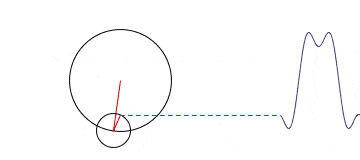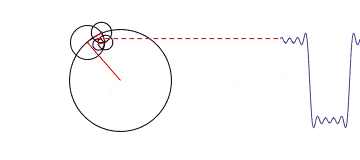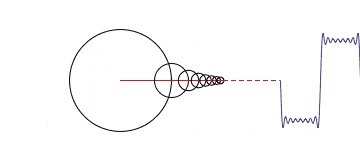
Another option is the use of the circumference interpretation instead of the sinusoid. For example, we have a set of circles of different sizes, where the center of each is on a circle of larger radius. Circles start spinning around; smaller circles spin around the bigger ones; smaller circles spin faster than the bigger If you follow up the motion of one point of the smallest circle, you can get a wave of any shape as it is shown in the picture below. So, Fourier transform tells how to build a wave and how the circles move towards one another.
This is not just another mathematical trick. Breaking waves into pieces, Fourier transforms shows almost everything what they make. Applications recognizing the songs (Shazam, Sound Hound, etc.) work according to this principle also. The music becomes broken into pieces so that the Fourier transform could be used to find sound components, which make up each piece. Then app searches songs, which have the same “fingerprint ” as the obtained file, in the database. Even the Speech Recognition uses the same idea, where sounds of speech are being compared to the sounds of the word corpuses.
We can list practical aspects of Fourier idea for a long time, but the fact which remains the same is that it’s a brilliant mathematical trick indeed.
